题目内容
 如图,在?ABCD中,AB=6cm,点P从点A出发,以1cm/s的速度向点B运动,点Q从点C出发,以2cm/s的速度向点D运动,当一个点运动到端点时,另一个点也停止运动,经过多长时间后,四边形APQD是平行四边形?
如图,在?ABCD中,AB=6cm,点P从点A出发,以1cm/s的速度向点B运动,点Q从点C出发,以2cm/s的速度向点D运动,当一个点运动到端点时,另一个点也停止运动,经过多长时间后,四边形APQD是平行四边形?考点:平行四边形的判定与性质
专题:动点型
分析:利用平行四边形的性质得出AB∥DC,AB=DC=6cm,进而利用平行四边形的判定方法得出即可.
解答:解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC=6cm,
当DQ=AP时,
QD
AP,则四边形APQD是平行四边形,
故设x秒时,QD=AP,则x=6-2x,
解得:x=2.
即2秒时,四边形APQD是平行四边形.
∴AB∥DC,AB=DC=6cm,
当DQ=AP时,
QD
| ∥ |
. |
故设x秒时,QD=AP,则x=6-2x,
解得:x=2.
即2秒时,四边形APQD是平行四边形.
点评:此题主要考查了平行四边形的判定与性质,正确掌握平行四边形的判定方法是解题关键.

练习册系列答案
相关题目
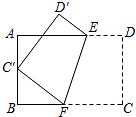 如图所示,将矩形ABCD沿直线EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )
如图所示,将矩形ABCD沿直线EF折叠,使顶点C恰好落在AB边的中点C′上,若AB=6,BC=9,则BF的长为( )| A、4 | ||
B、3
| ||
| C、4.5 | ||
D、2
|
线段AB被分为2:3:4三部分,已知第一部分和第三部分的中点间的距离是6.6cm,则线段AB的长为( )
| A、8.9cm |
| B、9.9cm |
| C、10.8cm |
| D、11.7cm |
|-3|的绝对值是( )
| A、-3 | ||
B、-
| ||
| C、3 | ||
| D、±3 |
 如图,在平面内有A、B、C三点.
如图,在平面内有A、B、C三点.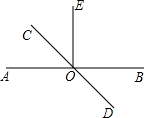 如图,直线AB和CD相交于点O,OE⊥AB,∠AOD=125°,则∠COE的度数是
如图,直线AB和CD相交于点O,OE⊥AB,∠AOD=125°,则∠COE的度数是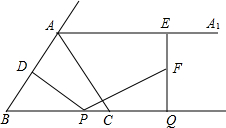 如图,△ABC中,AB=AC=5,BC=6,过点A作射线AAl∥BC.动点P从点B出发沿射线BC方向以每秒5个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒3个单位的速度运动.过点P作PD⊥AB于D,过点Q作QE⊥BC交射线AA1于E,F是QE中点,连结PF.设点P运动的时间为t秒.
如图,△ABC中,AB=AC=5,BC=6,过点A作射线AAl∥BC.动点P从点B出发沿射线BC方向以每秒5个单位的速度运动,同时动点Q从点C出发沿射线BC方向以每秒3个单位的速度运动.过点P作PD⊥AB于D,过点Q作QE⊥BC交射线AA1于E,F是QE中点,连结PF.设点P运动的时间为t秒.