题目内容
19.化简求值:当x=3,y=4时,求代数式$\frac{x-9y}{\sqrt{x}-3\sqrt{y}}$+$\frac{x+2\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}$的值.分析 首先对第一个式子的分子利用平方差公式分解,第二个式子利用完全平方公式分解,然后约分,合并同类二次根式即可化简,然后代入数值计算即可.
解答 解:原式=$\frac{(\sqrt{x}-3\sqrt{y})(\sqrt{x}+\sqrt{y})}{\sqrt{x}-3\sqrt{y}}$+$\frac{(\sqrt{x}+\sqrt{y})^{2}}{\sqrt{x}+\sqrt{y}}$
=$\sqrt{x}$+3$\sqrt{y}$+$\sqrt{x}$+$\sqrt{y}$
=2$\sqrt{x}$+4$\sqrt{y}$,
当x=3,y=4时,原式=2$\sqrt{3}$+4$\sqrt{4}$=2$\sqrt{3}$+8.
点评 本题考查了二次根式的化简求值,正确理解平方差公式和完全平方公式对分子进行变形是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若x2+ax-2y+7-(bx2-2x+9y-1)的值与x的无关,则-a-b的值为( )
| A. | 3 | B. | 1 | C. | -2 | D. | 2 |
7.下列方程是一元二次方程的是( )
| A. | ax2-2x+=0(a是已知数) | B. | 3x2+2x-4=3x2 | ||
| C. | 5x2-2x=0 | D. | $\frac{{x}^{3}+2x}{x}$=1 |
4.等腰三角形的两边分别为12和6,则这个三角形的周长是( )
| A. | 24 | B. | 18 | C. | 30 | D. | 24或30 |

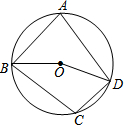 如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD=100°.
如图,四边形ABCD内接于⊙O,若∠BOD=160°,则∠BCD=100°.