题目内容
5.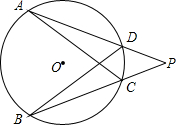 如图,∠P=40°,$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$,∠CAD等于( )
如图,∠P=40°,$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$,∠CAD等于( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
分析 连接AB,由$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$,得到∠ABD=∠ACB=∠BAC,根据外角的性质得到∠ACB=∠P+∠CAD=40°+∠CAD,根据三角形的内角和列方程即可得到结论.
解答  解:连接AB,∵$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$,
解:连接AB,∵$\widehat{AB}$=$\widehat{BC}$=$\widehat{DA}$,
∴∠ABD=∠ACB=∠BAC,
∵∠ACB=∠P+∠CAD=40°+∠CAD,
∴∠BAC=∠ABD=40°+∠CAD,
∵∠CAD=∠DBC,
∴∠ABC+∠ACB+∠BAC=3(40°+∠CAD)+∠CAD=180°,
∴∠CAD=15°,
故选B.
点评 本题考查了圆周角定理,圆心角、弧、弦的关系,三角形的内角和,连接AB构造三角形是解题的关键.

练习册系列答案
相关题目
17.已知M是关于x的五次多项式,N是关于x的三次多项式,则下列说法中正确的是( )
| A. | M+N是关于x的八次多项式 | B. | M-N是关于x的二次多项式 | ||
| C. | M+N与M-N都是关于x的五次多项式 | D. | M+N与M-N是几次多项式无法确定 |
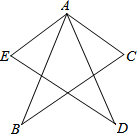 已知,如图,AE=AC,∠E=∠C,∠EAB=∠CAD,求证:AB=AD.
已知,如图,AE=AC,∠E=∠C,∠EAB=∠CAD,求证:AB=AD.