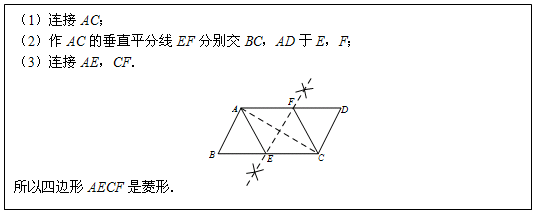
题目内容
10.一次函数y=-ax+b的图象经过二、三、四象限,则化简$\sqrt{{{(a-b)}^2}}+\sqrt{a^2}$,所得的结果是2a-b.分析 由一次函数y=-ax+b的图象经过二、三、四象限即可得出a>0、b<0,进而可得出a-b>0,依此将$\sqrt{{{(a-b)}^2}}+\sqrt{a^2}$化简即可得出结论.
解答 解:∵一次函数y=-ax+b的图象经过二、三、四象限,
∴-a<0,b<0,
∴a>0,a-b>0,
∴$\sqrt{(a-b)^{2}}$+$\sqrt{{a}^{2}}$=(a-b)+a=2a-b.
故答案为:2a-b.
点评 本题考查了一次函数图象与系数的关系以及二次根式的性质与化简,牢记“k<0,b<0?y=kx+b的图象在二、三、四象限”是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.小明在“践行中学生守则、争做优秀中学生”演讲比赛中,六位评委给他的分数如下表:
这组分数的众数是90.
| 评委代号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
| 评分 | 85 | 90 | 80 | 95 | 90 | 90 |

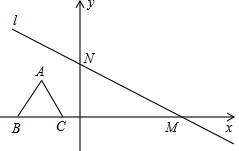 如图,在平面直角坐标系中,直线l:y=-$\frac{\sqrt{3}}{3}$x+4与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
如图,在平面直角坐标系中,直线l:y=-$\frac{\sqrt{3}}{3}$x+4与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题: 如图,如果正方形ABCD旋转后能与正方形CDFE重合,那么图形所在平面上可以作为旋转中心的点有3个.
如图,如果正方形ABCD旋转后能与正方形CDFE重合,那么图形所在平面上可以作为旋转中心的点有3个.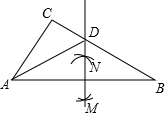 如图,在△ABC中,分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为14.
如图,在△ABC中,分别以点A,B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,若△ADC的周长为8,AB=6,则△ABC的周长为14.