题目内容
20．
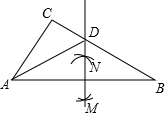如图，在△ABC中，分别以点A，B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，若△ADC的周长为8，AB=6，则△ABC的周长为14．
分析 由在△ABC中，分别以点A和点B为圆心，大于$\frac{1}{2}$AB的长为半径画弧，两弧相交于点M、N，作直线MN，可得MN是AB的垂直平分线，根据线段垂直平分线的性质，由△ADC的周长为8，即可得AC+BC=8，继而求得答案．
解答 解：根据题意得：MN是AB的垂直平分线，
∴AD=BD，
∵△ADC的周长为8，
∴AC+CD+AD=AC+CD+BD=AC+BC=8，
∵AB=6，
∴△ABC的周长为：AC+BC+AB=14．
故答案为14．
点评 此题考查了线段垂直平分线的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
11．北京市某一周的最高气温统计如表：
则这组数据的平均数是30，中位数是30．
| 日期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 最高气温（℃） | 31 | 29 | 28 | 30 | 31 | 30 | 31 |
5．在函数y=$\frac{\sqrt{x+1}}{x-2}$中，自变量x的取值范围是（ ）
| A． | x＞-1 | B． | x≥-1 | C． | x≥-1且x≠2 | D． | x＞-1且x≠2 |
12．
如图，二次函数y=ax2+bx+c的图象经过点（1，1）和点（3，0）．下列关于这个二次函数的描述，正确的是（ ）
如图，二次函数y=ax2+bx+c的图象经过点（1，1）和点（3，0）．下列关于这个二次函数的描述，正确的是（ ）| A． | y的最大值大于1 | B． | 当x=0时，y的值大于0 | ||
| C． | 当x=2时，y的值等于1 | D． | 当x＞3时，y的值大于0 |
8．
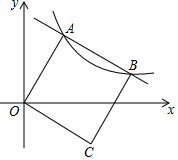如图，平面直角坐标系中，O为坐标原点，正方形OABC的定点A，B都在反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象上，边BC与x轴交于点D，则$\frac{BD}{CD}$的值为（ ）
如图，平面直角坐标系中，O为坐标原点，正方形OABC的定点A，B都在反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象上，边BC与x轴交于点D，则$\frac{BD}{CD}$的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{5}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{5}-1}{2}$ |
9．一幅平面图的比例尺是10：1，实际距离1厘米在这幅图上应画（ ）
| A． | 1毫米 | B． | 1厘米 | C． | 1分米 | D． | 10分米 |