��Ŀ����
5��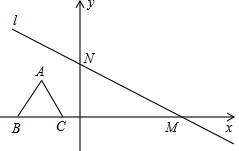 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=-$\frac{\sqrt{3}}{3}$x+4��x�ᡢy��ֱ��ڵ�M��N����Ϊ3�ĵȱ�������ABC����BC��x���ϣ���������������x���������ƽ�ƣ���ƽ�ƹ����У��õ���A1B1C1������B1��ԭ���غ�ʱ������������⣺
��ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=-$\frac{\sqrt{3}}{3}$x+4��x�ᡢy��ֱ��ڵ�M��N����Ϊ3�ĵȱ�������ABC����BC��x���ϣ���������������x���������ƽ�ƣ���ƽ�ƹ����У��õ���A1B1C1������B1��ԭ���غ�ʱ������������⣺��1�������A1�����꣬���жϵ�A1�Ƿ���ֱ��l�ϣ�
��2�������A1C1����ֱ�ߵĽ���ʽ��
��3��������ƽ������һ��P��ʹ����P��A1��C1��MΪ������ı�����ƽ���ı��Σ���ֱ��д��P�����꣮
���� ��1����ͼ��A1H��x����H����Rt��A1OH�У���A1H=3����A1OH=60�㣬�ɵ�OH=A1H•tan30��=$\sqrt{3}$�������A���꼴�ɽ�����⣻
��2�����ô���ϵ�������ɽ�����⣻
��3���������������ۼ��ɽ�����⣻
��� �⣺��1��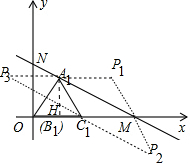 ��ͼ��A1H��x����H��
��ͼ��A1H��x����H��
��Rt��A1OH�У���A1H=3����A1OH=60�㣬
��OH=A1H•tan30��=$\sqrt{3}$��
��A1��$\sqrt{3}$��3����
��x=$\sqrt{3}$ʱ��y=-$\frac{\sqrt{3}}{3}$��$\sqrt{3}$+4=3��
��A1��ֱ��y=-$\frac{\sqrt{3}}{3}$x+4�ϣ�
��2����A1��$\sqrt{3}$��3����C1��2$\sqrt{3}$��0����
��ֱ��A1C1�Ľ���ʽΪy=kx+b������$\left\{\begin{array}{l}{\sqrt{3}k+b=3}\\{2\sqrt{3}k+b=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\sqrt{3}}\\{b=6}\end{array}\right.$��
��ֱ��A1C1�Ľ���ʽΪy=-$\sqrt{3}$x+6��
��3����M��4$\sqrt{3}$��0����A1��$\sqrt{3}$��3����C1��2$\sqrt{3}$��0����
��ͼ���֪������P��A1��C1��MΪ������ı�����ƽ���ı���ʱ��P1��3$\sqrt{3}$��3����P2��5$\sqrt{3}$��-3����P3��-$\sqrt{3}$��3����
���� ���⿼��һ�κ����ۺ��⣮ƽ���ı��ε��ж������ʡ�����ϵ������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬�����п��������ͣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�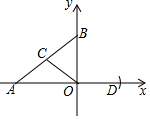 ��ͼ���ڡ�ABO�У�A��-4��0����B��0��3����OCΪAB�ߵ����ߣ���OΪԲ�ģ��߶�OC��Ϊ�뾶��������x���������ڵ�D�����D������Ϊ��$\frac{5}{2}$��0����
��ͼ���ڡ�ABO�У�A��-4��0����B��0��3����OCΪAB�ߵ����ߣ���OΪԲ�ģ��߶�OC��Ϊ�뾶��������x���������ڵ�D�����D������Ϊ��$\frac{5}{2}$��0���� ��ͼ���ڡ�ABC�У�AB=3��AC=6������ABC�Ƶ�C����ʱ�뷽����ת�õ���A1B1C��ʹCB1��AD���ֱ��ӳ�AB��CA1�ཻ�ڵ�D�����߶�BD�ij�Ϊ9��
��ͼ���ڡ�ABC�У�AB=3��AC=6������ABC�Ƶ�C����ʱ�뷽����ת�õ���A1B1C��ʹCB1��AD���ֱ��ӳ�AB��CA1�ཻ�ڵ�D�����߶�BD�ij�Ϊ9��