题目内容

19．已知：如图，AD∥BC，∠B=∠D，求证：∠E=∠F．

分析 根据平行线的性质得到∠DAB+∠B=∠BCD+∠D=180°，∠2=∠3，等量代换得到∠DAB=∠BCD，根据对顶角的性质得到∠1=∠2，∠3=∠4，等量代换得到∠1=∠4，根据三角形的外角的性质得到∠E=∠DAB-∠1，∠F=∠BCD-∠4，于是得到结论．

解答 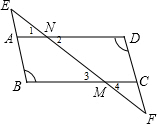证明：∵AD∥BC，
∴∠DAB+∠B=∠BCD+∠D=180°，∠2=∠3，
∵∠B=∠D，
∴∠DAB=∠BCD，
∵∠1=∠2，∠3=∠4，
∴∠1=∠4，
∴∠E=∠DAB-∠1，∠F=∠BCD-∠4，
∴∠E=∠F．

点评 此题主要查了平行线的性质与判定以及三角形内角和定理等知识，熟练正确平行线的性质是解决问题的关键．

练习册系列答案
相关题目
9．一元二次方程x2-8x+12=0的两个根是等腰三角形的两条边长，则该等腰三角形的周长是14．
10．如图，边长为1的正方形ABCD的顶点A在y轴上，B在x轴上，将正方形ABCD平移，使点A与点C重合，得正方形CEFG，己知∠OAB=30°，则点G的坐标为（$\frac{1}{2}+\sqrt{3}$，1）．
7．计算题
（1）$\frac{1}{4}$x2y×（-2xy2）    
（2）（-1）2014-（3-π）0+（-$\frac{1}{3}$）-2
（3）2011×2013-20122
（4）（4a3b-6a3b2-10ab2）÷（2ab）
14．下列方程，是一元一次方程的是（　　）
A．x-y=5B．x2+x+6=0C．x-7D．$\frac{2}{3}$x=5
4．观察下列方程及其解的特征：
①x+$\frac{1}{x}=2+\frac{1}{2}$的解为x1=2，x2=$\frac{1}{2}$；
②x+$\frac{1}{x}=3+\frac{1}{3}$的解为x1=3，x2=$\frac{1}{3}$；
③x+$\frac{1}{x}=4+\frac{1}{4}$的解为x1=4，x2=$\frac{1}{4}$；
…
解答下列问题：
（1）根据解的特征，猜测方程x+$\frac{1}{x}=-\frac{5}{2}$的解为x1=-2，x2=-$\frac{1}{2}$，并写出解答过程；
（2）直接写出关于x的分式方程2x+$\frac{1}{2x-5}=\frac{{{a^2}+5a+1}}{a}$的解为x1=$\frac{a+5}{2}$，x2=$\frac{1}{2a}$+$\frac{5}{2}$．．
11．计算：
（1）（-$\sqrt{3}$）2-$\sqrt{\frac{1}{4}}$-$\root{3}{-0.125}$+$\sqrt{（-4）^{2}}$-|-6|
（2）|1-$\sqrt{2}$|+|$\sqrt{2}$-$\sqrt{3}$|+|$\sqrt{3}$-2|．
（3）4（x+3）2-16=0
（4）27（x-3）3=-8．
8．如图，AB是⊙O的直径，∠BOC=50°，则∠D的度数为（　　）
A．65°B．25°C．15°D．35°
9．已知：${（a+b）^2}+\sqrt{{b^2}-2b-3}=0$，则ab2-4b-a的值为36或4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网