Question

1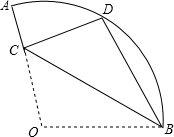．如图，在扇形OAB中，∠AOB=110°，将扇形OAB沿过点B的直线折叠，点O恰好落在$\widehat{AB}$上的点D处，折痕交OA于点C，则$\widehat{AD}$的度数为（　　）

• A． 40°
• B． 50°
• C． 60°
• D． 70°

Answer 1

分析 连结OD，先根据折叠的性质得到BC垂直平分OD，则BD=BO，易得△OBD为等边三角形，所以∠DOB=60°，则∠AOD=∠AOB-∠DOB=50°．

解答 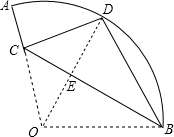解：连结OD，如图，
∵扇形OAB沿过点B的直线折叠，点O恰好落在$\widehat{AB}$上的点D处，折痕交OA于点C，
∴BC垂直平分OD，
∴BD=BO，
∵OB=OD，
∴△OBD为等边三角形，
∴∠DOB=60°，
∴∠AOD=∠AOB-∠DOB=110°-60°=50°，
∴$\widehat{AD}$的度数为为50°，
故选：B．

点评 本题考查了圆周角定理和折叠的性质，解题时注意：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．