题目内容
19.已知,坐标系中,A(0,1),B(0,-2),C(3,0).(1)在第二、四象限角平分线上找一点D,使||AD|-|BD||最大,求最大值,并通过作图写出点D的坐标;
(2)在第二、四象限角平分线上找一点E,使|AE|+|BE|最小,求最小值,并通过作图写出点E的坐标.
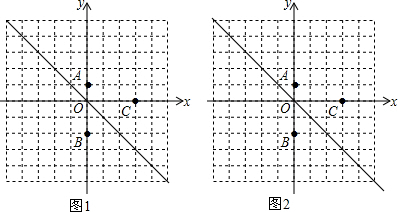
分析 (1)求得点B(0,-2)关于第二、四象限角平分线的对称点B′的坐标为(2,0),连接B'A并延长交角平分线于点D,连接DB.此时BD=BD′,根据三角形三边关系即可证得||AD|-|BD||最大,最大值为AB′;
(2)连接AB,交关于第二、四象限角平分线于E,此时|AE|+|BE|最小,最小值为AB.
解答 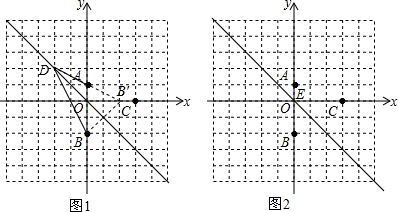 解:(1)如图1,∵B(0,-2)关于第二、四象限角平分线的对称点B′的坐标为(2,0),连接B'A并延长交 角平分线于点D,连接DB.
解:(1)如图1,∵B(0,-2)关于第二、四象限角平分线的对称点B′的坐标为(2,0),连接B'A并延长交 角平分线于点D,连接DB.
此时||AD|-|BD||最大,最大值为AB′=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$;
由作图可知,D(-2,2).
(2)如图2,连接AB,交关于第二、四象限角平分线于E,
此时|AE|+|BE|最小,最小值为AB=1+2=3.
由作图可知,E(0,0).
点评 本题考查了轴对称-最短路线问题,作出D、E的位置是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.在Rt△ABC和Rt△A′B′C′,∠C=∠C′=90°,AC=A′C′,AB=A′B′,下列结论错误的是( )
| A. | ∠A=∠A′ | B. | BC=B′C′ | C. | AC=B′C′ | D. | ∠B=∠B′ |
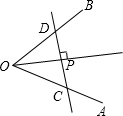 如图所示,OP平分∠AOB,过点P作OP的垂线分别交OA,OB于点C,D,问PC=PD吗?为什么?
如图所示,OP平分∠AOB,过点P作OP的垂线分别交OA,OB于点C,D,问PC=PD吗?为什么? 分别输入-4,-2,按如图所示的程序运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),写出输出的结果.
分别输入-4,-2,按如图所示的程序运算(完成一个方框内的运算后,把结果输入下一个方框继续进行运算),写出输出的结果.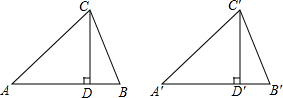 如图,已知在△ABC和△A′B′C′中,CD,C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.求证:△ABC≌△A′B′C′.
如图,已知在△ABC和△A′B′C′中,CD,C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′.求证:△ABC≌△A′B′C′.