题目内容
7.用反证法证明:垂直于同一条直线的两条直线互相平行.分析 写出已知,求证,然后根据反证法的步骤给出证明即可解决问题.
解答 已知,在同一平面内有三条直线a,b,c,a⊥c,b⊥c.求证:a∥b.
证明:假设所求证的结论不成立,即a与b不平行,
则直线a与b相交,设它们的焦点为O.
因为a⊥c,b⊥c,则过O点有两条直线a,b与直线c垂直,
这与过一点有且只有一条直线与已知直线垂直相矛盾,
所以假设不成立,
所求证的结论成立.
点评 本题考查反证法,记住反证法分步骤是解题的关键,记住反证法的第一步是假设结论不成立,然后推出与已知或定理矛盾,最后强调假设不成立,结论成立,属于中考常考题型.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
9.若一个多边形的每一个内角与外角的比都是4:1,那么这个多边形的边数是( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
12.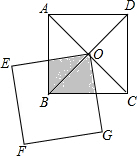 如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
 如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )
如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点旋转,若两个正方形的边长相等,则两个正方形的重合部分的面积( )| A. | 由小变大 | B. | 由大变小 | ||
| C. | 始终不变 | D. | 先由大变小,然后又由小变大 |