题目内容
△ABC的三边AB,BC,CA的长分别为6cm,4cm,4cm,P为三边角平分线的交点,则△ABP,△BCP,△ACP的面积比等于( )
| A、1:1:1 |
| B、2:2:3 |
| C、2:3:2 |
| D、3:2:2 |
考点:角平分线的性质
专题:
分析:根据角平分线上的点到角的两边距离相等可得点P到△ABC三边的距离相等,然后根据等高的三角形的面积的比等于底边的比解答.
解答:解:∵P为三边角平分线的交点,
∴点P到△ABC三边的距离相等,
∵AB,BC,CA的长分别为6cm,4cm,4cm,
∴△ABP,△BCP,△ACP的面积比=6:4:4=3:2:2.
故选D.
∴点P到△ABC三边的距离相等,
∵AB,BC,CA的长分别为6cm,4cm,4cm,
∴△ABP,△BCP,△ACP的面积比=6:4:4=3:2:2.
故选D.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,等高的三角形的面积的比等于底边的比,熟记性质并判断出点P到△ABC三边的距离相等是解题的关键.

练习册系列答案
相关题目
把一条弯曲的公路改直,可以缩短行程,这样做的依据是( )
| A、线段可以比较大小 |
| B、线段有两个端点 |
| C、两点确定一条直线 |
| D、两点之间线段最短 |
抛物线y=a(x-3)2+4交y轴于点C,BC∥x轴交抛物线于点B,则线段BC的长为( )
| A、3 | B、6 | C、3a | D、6a |
下列运算正确的是( )
| A、a+a=2a2 |
| B、a2•a=2a2 |
| C、(2a)2÷a=4a |
| D、(-ab)2=2ab2 |
以下列数组为边长中,能构成直角三角形的是( )
| A、6,7,8 | ||||||
| B、0.2,0.3,0.5 | ||||||
C、1,1,
| ||||||
D、
|
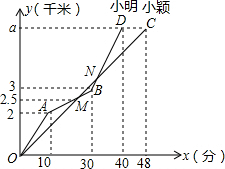 为参加某市冬季越野赛,小明、小强两名同学进行了a千米的越野跑训练,在越野跑训练中的路程y(千米)与时间x(分)函数关系如图所示.
为参加某市冬季越野赛,小明、小强两名同学进行了a千米的越野跑训练,在越野跑训练中的路程y(千米)与时间x(分)函数关系如图所示.