题目内容
4.已知矩形ABCD的边AB=a,AD=b(a>b>0),若点P为CD边上的一动点,且记DP=x,直线AP交BC的延长线于Q,使得DP+CQ为最小时,a,b、x应满足关系式为( )| A. | x=$\frac{a+b}{2}$ | B. | x=$\sqrt{ab}$ | C. | a2-b2=x2 | D. | $\frac{1}{x}$=$\frac{1}{a}$+$\frac{1}{b}$ |
分析 由PC∥AB得$\frac{PC}{AB}=\frac{CQ}{BQ}$,所以$\frac{a-x}{a}=\frac{CQ}{CQ+b}$,所以CQ=$\frac{ab}{x}-b$,所以DP+CQ=x+$\frac{ab}{x}-b$≥2$\sqrt{ab}$-b,当x=$\frac{ab}{x}$时,DP+CQ的值最小,由此即可解决问题.
解答 解:如图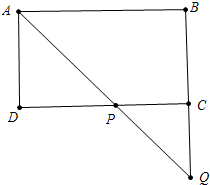 ,∵四边形ABCD是矩形,
,∵四边形ABCD是矩形,
∴AB=CD=a,AD=BC=b,AB∥CD,
∵PC∥AB,
∴$\frac{PC}{AB}=\frac{CQ}{BQ}$,
∴$\frac{a-x}{a}=\frac{CQ}{CQ+b}$,
∴CQ=$\frac{ab}{x}-b$,
∴DP+CQ=x+$\frac{ab}{x}-b$≥2$\sqrt{ab}$-b,
∴当x=$\frac{ab}{x}$时,DP+CQ的值最小,
∴x2=ab,
∴x=$\sqrt{ab}$.
故选B.
点评 本题考查矩形的性质、平行线分线段成比例定理,不等式的性质即a+b≥2$\sqrt{ab}$(a≥0,b≥0)且a=b时等号成立,灵活运用不等式性质是解决最值的关键.

练习册系列答案
相关题目
15.若ab=-3,a-2b=5,则a2b-2ab2的值是( )
| A. | -15 | B. | 15 | C. | 2 | D. | -8 |
16.一次函数y=x-1的图象向上平移2个单位后,不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.计算:(-1)100×5的结果是( )
| A. | -1 | B. | 5 | C. | 100 | D. | 500 |
 如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$.
如图,矩形ABCD中,AB=6,BC=8,点F为BC边上的一个动点,把△ABF沿AF折叠.当点B的对应点B′落在矩形ABCD的对称轴上时,则BF的长为$2\sqrt{3}$或$9-3\sqrt{5}$. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,$\widehat{BC}=\widehat{PC}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,$\widehat{BC}=\widehat{PC}$.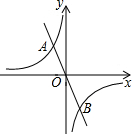 如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A,B,若点A的坐标为(-2,3),则点B的坐标为(2,-3).
如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A,B,若点A的坐标为(-2,3),则点B的坐标为(2,-3). (1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=$\sqrt{2}$.
(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=$\sqrt{2}$.