题目内容
19．
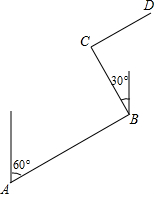幸福乡要修建一条灌溉水渠，如图，水渠从A村沿北偏东60°的方向到B村，从B村沿北偏西30°方向到C村．若水渠从C村沿CD方向修建可以保持与AB的方向一致，则∠DCB的度数为90°．
分析 利用平行线的判定得出CD∥BE，可得∠NCD=30°+60°=90°，进而得出∠DCB的度数即可得出答案．
解答 
解：如图所示：
由题意可得：∠1=60°，
当CD保持与AB的方向一致，
则CD∥BE，
则∠NCD=30°+60°=90°，
故∠DCB=180°-90°=90°．
故答案为：90．
点评 此题主要考查了方向角以及平行线的性质，得出∠NCD的度数是解题关键．
练习册系列答案
考前必练系列答案
相关题目
9．
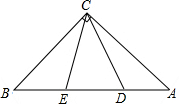如图，在等腰直角△ABC中，AC=BC，∠BCA=90°，D、E为斜边AB上的点，∠DCE=45°，若AD=2，DE=5，则BE的长是（ ）
如图，在等腰直角△ABC中，AC=BC，∠BCA=90°，D、E为斜边AB上的点，∠DCE=45°，若AD=2，DE=5，则BE的长是（ ）| A． | 3 | B． | $\frac{9}{2}$ | C． | $\sqrt{19}$ | D． | $\sqrt{21}$ |
10．
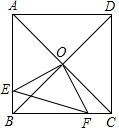如图，在正方形ABCD中．O是对角线AC、BD的交点．过点O作OE⊥OF，分别交AB、BC于点E，F．若AE=3，CF=1，则EF=（ ）
如图，在正方形ABCD中．O是对角线AC、BD的交点．过点O作OE⊥OF，分别交AB、BC于点E，F．若AE=3，CF=1，则EF=（ ）| A． | 2 | B． | $\sqrt{10}$ | C． | 4 | D． | 2$\sqrt{2}$ |
如图，点A（1，2），点B在x轴上，AO=AB，若双曲线y=$\frac{k}{x}$与边OA，AB分别相交于C，D两点，且OC=2BD，则实数k的值为8．