题目内容
11.若x2+x-1=0,则$\frac{{x}^{4}+(x-1)^{2}-1}{x(x-1)}$的值为3.分析 由x2+x-1=0得到x2=-(x-1),将$\frac{{x}^{4}+(x-1)^{2}-1}{x(x-1)}$变形为$\frac{2(x-1)^{2}-1}{x(x-1)}$,进一步得到原式=$\frac{2{x}^{2}-4x+1}{{x}^{2}+x-2x}$=$\frac{2(1-x)-4x+1}{1-2x}$,再化简后约分计算即可求解.
解答 解:∵x2+x-1=0
∴x2=-(x-1),
∴$\frac{{x}^{4}+(x-1)^{2}-1}{x(x-1)}$
=$\frac{2(x-1)^{2}-1}{x(x-1)}$
=$\frac{2{x}^{2}-4x+1}{{x}^{2}+x-2x}$
=$\frac{2(1-x)-4x+1}{1-2x}$
=$\frac{3(1-2x)}{1-2x}$
=3.
故答案为:3.
点评 考查了分式的值,分式求值历来是各级考试中出现频率较高的题型,而条件分式求值是较难的一种题型,在解答时应从已知条件和所求问题的特点出发,通过适当的变形、转化,才能发现解题的捷径.

练习册系列答案
相关题目
1.如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.
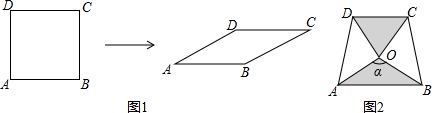
(1)请补全表:
(2)填空:由(1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把单位菱形的面积S记为S(α).例如:当α=30°时,S=S(30°)=$\frac{1}{2}$;当α=135°时,S=S=$\frac{\sqrt{2}}{2}$.由上表可以得到S(60°)=S(120°);S(30°)=S(30°),…,由此可以归纳出S(α)=(α°).
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).

(1)请补全表:
| α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
| S | $\frac{1}{2}$ | 1 | $\frac{\sqrt{2}}{2}$ |
(3)两块相同的等腰直角三角板按图2的方式放置,AD=$\sqrt{2}$,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
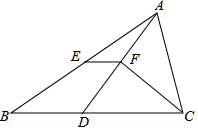 如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
如图.在△ABC中,BC>AC,点D在BC上,且CD=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.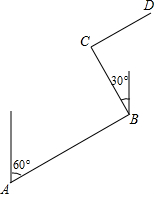 幸福乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东60°的方向到B村,从B村沿北偏西30°方向到C村.若水渠从C村沿CD方向修建可以保持与AB的方向一致,则∠DCB的度数为90°.
幸福乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东60°的方向到B村,从B村沿北偏西30°方向到C村.若水渠从C村沿CD方向修建可以保持与AB的方向一致,则∠DCB的度数为90°. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.