题目内容
8．已知圆锥的底面半径是3，母线长为10，则圆锥侧面展开后所得扇形的圆心角是108°．分析 求得圆锥的底面周长即为侧面扇形的弧长，利用弧长公式即可求得扇形的圆心角．
解答 解：圆锥的底面周长为：2π×3=6π，
那么$\frac{nπ×10}{180}$=6π，
解得n=108°．
故答案是：108°．
点评 本题考查了圆锥的计算，正确理解圆锥母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长是关键．
练习册系列答案
相关题目
19．
如图，工人师傅为了固定长方形的木架，通常加两根木条，使其不变形，这种做法的根据是（ ）
如图，工人师傅为了固定长方形的木架，通常加两根木条，使其不变形，这种做法的根据是（ ）| A． | 三角形的内角和为180° | B． | 两点之间线段最短 | ||
| C． | 三角形的稳定性 | D． | 直角三角形两锐角互余 |
16．
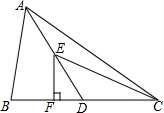在△ABC中，AD是BC边上的中线，点E是AD中点，过点E作垂线交BC于点F，已知BC=10，△ABD的面积为12，则EF的长为（ ）
在△ABC中，AD是BC边上的中线，点E是AD中点，过点E作垂线交BC于点F，已知BC=10，△ABD的面积为12，则EF的长为（ ）| A． | 1.2 | B． | 2.4 | C． | 3.6 | D． | 4.8 |
实验室里，水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器（容器足够高），底面半径之比为1：2：1，用两个相同的管子在10cm高度处连通（即管子底部离容器底10cm），现三个容器中，只有乙中有水，水位高4cm，如图所示．若每分钟同时向甲和丙注入相同量的水，开始注水1分钟，甲的水位上升3cm．则开始注入$\frac{5}{3}$或$\frac{20}{3}$分钟水量后，甲的水位比乙高1cm．
20．对于二次函数y=2x2-8x+6的图象，下列说法正确的是（ ）
| A． | 开口向下 | B． | 与x轴的交点横坐标是x1=-1，x2=-3 | ||
| C． | 对称轴是直线x=-2 | D． | 由y=-2（x-2）2+2的图象轴对称得到 |
17．
如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，下列结论中错误的是（ ）
如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，下列结论中错误的是（ ）| A． | AC2=AD•AB | B． | CD2=CA•CB | C． | CD2=AD•DB | D． | BC2=BD•BA |