题目内容
18．若（x-1）（x+3）=x2+mx+n，则m+n=（ ）| A． | -1 | B． | -2 | C． | -3 | D． | 2 |
分析 已知等式左边利用多项式乘以多项式法则计算，再利用多项式相等的条件求出m与n的值，即可求出m+n的值．
解答 解：已知等式整理得：（x-1）（x+3）=x2+2x-3=x2+mx+n，
∴m=2，n=-3，
则m+n=2-3=-1．
故选A
点评 此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
6．设a=2$\sqrt{3}$-1，a在两个相邻整数之间，则这两个整数是（ ）
| A． | 1和2 | B． | 2和3 | C． | 3和4 | D． | 4和5 |
3．
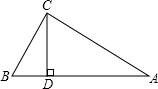如图，已知Rt△ABC中，∠ACB=90°，CD是高，∠A=30°，BD=2cm，求AB的长（ ）
如图，已知Rt△ABC中，∠ACB=90°，CD是高，∠A=30°，BD=2cm，求AB的长（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 10 |
7．
如图，△ABC中，D为AB的中点，DE∥BC，则下列结论中错误的是（ ）
如图，△ABC中，D为AB的中点，DE∥BC，则下列结论中错误的是（ ）| A． | $\frac{AD}{BD}=\frac{DE}{BC}$ | B． | $\frac{AD}{BD}=\frac{AE}{EC}$ | ||
| C． | DE=$\frac{1}{2}$BC | D． | S△ADE=$\frac{1}{3}$S四边形BCED |
如图，已知直线y=4-x与反比例函数y=$\frac{m}{x}$（m＞0，x＞0）的图象交于A，B两点，且点A的横坐标为1，与x轴，y轴分别相交于C，D两点．