题目内容
13.在△ABC中,AB=AC,点D在BA的延长线上,AD=BC,连接DC,∠ADC=30°,则∠BAC为60度.分析 作AE⊥DC于E,AF⊥BC于F,利用条件可证得Rt△AEC≌Rt△CFA,得到CE=AF,再结合条件证得四边形AECF是矩形,从而可求得∠BAC.
解答 解:如图,作AE⊥DC于E,AF⊥BC于F,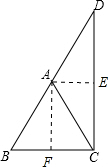
∵∠D=30°,
∴AE=$\frac{1}{2}$AD,
∵AB=AC,AF⊥BC,
∴BF=CF=$\frac{1}{2}$BC,
∵AD=BC,
∴AE=CF,
又∵∠AEC=∠CFA=90°,AC=CA
在△AEC和△CFA中,
$\left\{\begin{array}{l}{AE=CF}\\{AC=CA}\end{array}\right.$,
∴Rt△AEC≌Rt△CFA(HL),
∴CE=AF,
又∵AE=CF,∠AFC=90°,
∴四边形AECF是矩形,
∴∠ECF=90°,
则∠B=60°,
∵AB=AC,
∴△ABC是等边三角形,
∴∠BAC=60°,
故答案为:60°.
点评 本题主要考查等腰三角形的性质及矩形的判定和性质,构造三角形全等证明四边形AECF是矩形是解题的关键.

练习册系列答案
相关题目
1.合肥54中秉承了“爱心、耐心、理智、宽容”的办学宗旨.其寄宿制和小班化的两大办学特色,赢得了社会各界的关注和好评.自创校招生以来,每年报名人数均创新高.已知我校2011年招生750人,2013年招生1080人,如每年招生的增长率相同,请你预计今年的招生人数约为( )
| A. | 1100人 | B. | 1200人 | C. | 1300人 | D. | 1400人 |
18.若(x-1)(x+3)=x2+mx+n,则m+n=( )
| A. | -1 | B. | -2 | C. | -3 | D. | 2 |
 我们知道,已知圆心和半径,可以作一个圆.不难理解,经过一个已知点A作圆,能作出无数个.回答下列问题:
我们知道,已知圆心和半径,可以作一个圆.不难理解,经过一个已知点A作圆,能作出无数个.回答下列问题: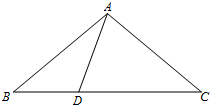 在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°. 如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=10,则PD=5.
如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=10,则PD=5. 作图题:(不写作法,但要保留痕迹)
作图题:(不写作法,但要保留痕迹) 已知三角形ABC的三个顶点A、B、C的坐标分别是(0,2)、(-3,0)、(1,-2),在下图的平面直角坐标系中表示出来,并根据图形回答下列问题.
已知三角形ABC的三个顶点A、B、C的坐标分别是(0,2)、(-3,0)、(1,-2),在下图的平面直角坐标系中表示出来,并根据图形回答下列问题.