题目内容
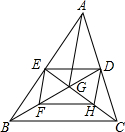 △ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,连接DE、EF、F、HD.
△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,连接DE、EF、F、HD.(1)求证:四边形DEFH为平行四边形;
(2)连接AG.
①当AG与BC具有什么关系时,四边形DEFH是菱形并证明;
②当AG与BC具有什么关系时,四边形DEFH是矩形.
考点:中点四边形
专题:
分析:(1)由△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,根据三角形中位线的性质,可得DE∥FH,DE=FH,即可证得四边形DEFH为平行四边形;
(2)①当AG=BC时,易证得EF=ED,又由四边形DEFH为平行四边形,即可判定四边形DEFH是菱形;
②当AG⊥BC时,易得ED⊥EF,又由四边形DEFH为平行四边形,即可判定四边形DEFH是矩形.
(2)①当AG=BC时,易证得EF=ED,又由四边形DEFH为平行四边形,即可判定四边形DEFH是菱形;
②当AG⊥BC时,易得ED⊥EF,又由四边形DEFH为平行四边形,即可判定四边形DEFH是矩形.
解答:证明:(1)∵△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,
∴DE∥BC,DE=
BC,FH∥BC,FH=
BC,
∴DE∥FH,DE=FH,
∴四边形DEFH为平行四边形;
(2)①当AG=BC时,四边形DEFH是菱形.
理由:∵△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,
∴EF=
AG,
∵DE=
BC,
∴当AG=BC时,EF=ED,
∵四边形DEFH为平行四边形,
∴?DEFH为菱形;
②当AG⊥BC时,四边形DEFH为矩形,
理由:∵△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,
∴DE∥FH∥BC,EF∥AG∥DH,
∴当AG⊥BC时,ED⊥EF,
∴∠DEF=90°,
∵四边形DEFH是平行四边形,
∴四边形DEFH是矩形.
∴DE∥BC,DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DE∥FH,DE=FH,
∴四边形DEFH为平行四边形;
(2)①当AG=BC时,四边形DEFH是菱形.
理由:∵△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,
∴EF=
| 1 |
| 2 |
∵DE=
| 1 |
| 2 |
∴当AG=BC时,EF=ED,
∵四边形DEFH为平行四边形,
∴?DEFH为菱形;
②当AG⊥BC时,四边形DEFH为矩形,
理由:∵△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,
∴DE∥FH∥BC,EF∥AG∥DH,
∴当AG⊥BC时,ED⊥EF,
∴∠DEF=90°,
∵四边形DEFH是平行四边形,
∴四边形DEFH是矩形.
点评:此题考查了中点四边形的性质、平行四边形的性质与判定、矩形的判定以及菱形的判定.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若菱形ABCD的对角线AC、BD交于点O,且AC=16,BD=12,则菱形的边长为( )
| A、10 | B、12 | C、28 | D、40 |
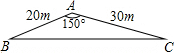
 如图所示的是一块从一边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,求这块垫片的周长.
如图所示的是一块从一边长为50cm的正方形材料中裁出的垫片,现测得FG=9cm,求这块垫片的周长.
 某市在旧城改造中,计划在市内一块如图所示三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要
某市在旧城改造中,计划在市内一块如图所示三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要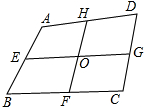 在四边形ABCD中,点E,F,G,H,分别是AB,BC,CD,DE的中点,EG与FH相交于O点.
在四边形ABCD中,点E,F,G,H,分别是AB,BC,CD,DE的中点,EG与FH相交于O点.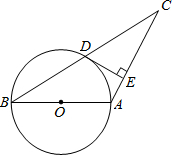 如图,AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E.
如图,AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E.