题目内容
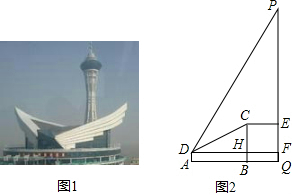
杭州跨海大桥海天一洲观景平台景色优美,如图1.现测量人员在船上测量观光塔高PQ,在海上的D处测得塔顶P的顶角∠PDF为80°,又测得塔底座边沿一处C的仰角∠CDH为30°,C处的海拔高度CB=12米,到中轴线PQ的距离CE为10米,测量仪的海拔高度AD=2米,DF⊥CB于H,交PQ于F,求观光塔的海拔高度PQ.(精确到0.1米,tan80°≈5.7,sin80°≈0.98,cos80°≈0.17,
≈1.73)
| 3 |

考点:解直角三角形的应用-仰角俯角问题
专题:
分析:首先利用锐角三角函数关系得出DH的高,进而求出PF的高,即可得出答案.
解答:解:由题意可得:AD=BH=2m,CH=BC-BH=10m,则EC=CH,故四边形CHFE是正方形,
∵∠CDH=30°,
∴tan30°=
=
=
,
解得:DH=10
,
故DF=(10
+10)m,则tan80°=
=
=5.7,
解得:EF≈155.7,
故PQ=EF+2=157.7(m).
答:观光塔的海拔高度PQ为157.7m.
∵∠CDH=30°,
∴tan30°=
| CH |
| DH |
| ||
| 3 |
| 10 |
| DH |
解得:DH=10
| 3 |
故DF=(10
| 3 |
| PF |
| DF |
| PF | ||
10
|
解得:EF≈155.7,
故PQ=EF+2=157.7(m).
答:观光塔的海拔高度PQ为157.7m.
点评:此题主要考查了解直角三角形的应用,正确应用锐角三角函数关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示是y关于x的函数图象,则当y=0时,x的值为( )
如图所示是y关于x的函数图象,则当y=0时,x的值为( )| A、-1 | B、1 |
| C、3 | D、-1或1或3 |
在Rt△ABC中,∠C=90°,sinA=
,则cosB的值为( )
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
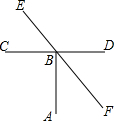 如图,AB⊥CD于B,EF是经过B点的一条直线,若∠EBD=135°,则∠ABF=( )
如图,AB⊥CD于B,EF是经过B点的一条直线,若∠EBD=135°,则∠ABF=( )| A、30° | B、45° |
| C、60° | D、75° |
已知|a|=5,b的倒数为-
,则a+b的值为( )
| 1 |
| 4 |
| A、1 | B、-9 | C、1或-9 | D、±5 |
 如图所示,在△ABC中,CD⊥AB于点D,若AB=5,CD=2
如图所示,在△ABC中,CD⊥AB于点D,若AB=5,CD=2 如图,在一块长为am,宽为bm的长方形草地上,有一条弯曲的小路,小路左边线向右平移1m就是它的右边线,求这块草地的绿地面积.
如图,在一块长为am,宽为bm的长方形草地上,有一条弯曲的小路,小路左边线向右平移1m就是它的右边线,求这块草地的绿地面积.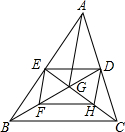 △ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,连接DE、EF、F、HD.
△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,连接DE、EF、F、HD.