题目内容
若菱形ABCD的对角线AC、BD交于点O，且AC=16，BD=12，则菱形的边长为（ ）
| A、10 | B、12 | C、28 | D、40 |
考点：菱形的性质
专题：
分析：根据菱形的对角线互相垂直平分，可知AO和BO的长，再根据勾股定理即可求得AB的值，又菱形的四条边相等，继而求出菱形的周长．
解答：
解：∵AC=16，BD=12，菱形对角线互相垂直平分，
∴AO=8，BO=6，
∴AB=
=10，
∴BC=CD=AD=AB=10，
∴菱形的周长为4×10=40．
解：∵AC=16，BD=12，菱形对角线互相垂直平分，∴AO=8，BO=6，
∴AB=
| OA2+OB2 |
∴BC=CD=AD=AB=10，
∴菱形的周长为4×10=40．
点评：本题考查了菱形对角线互相垂直平分的性质，考查了菱形各边长相等的性质，考查了勾股定理在直角三角形中的运用，根据勾股定理求AB的值是解题的关键．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
一粒芝麻约有0.000002千克，0.000002用科学记数学法表示为（ ）千克．
| A、2×10-4 |
| B、0.2×10-5 |
| C、2×10-7 |
| D、2×10-6 |
已知：如图，⊙O是△ABC的外接圆，AD⊥BC于D，AE平分∠BAC交⊙O于E，求证：AE平分∠OAD．
如图，点P从点A出发沿着线段AB向点B匀速运动，点P出发4分钟时距A地240cm，此时点Q也从点A沿着线段AB向点B匀速运动，再经过6分钟点Q追上点P，又经过2分钟点Q到达点B处，此时点P、Q同时停止运动，设点P的运动时间为t分钟．
如图所示是y关于x的函数图象，则当y=0时，x的值为（ ）| A、-1 | B、1 |
| C、3 | D、-1或1或3 |
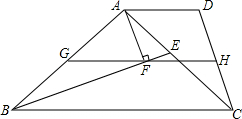如图，在梯形ABCD中，AD∥BC，BE是△ABC的角平分线，AF⊥BE于F，过F作GH∥BC分别交AB，CD于G，H．求证：
为了加强公民的节约意识，我市出台阶梯电价计算方案：（如下图）居民生活用电将月用电量分为三档，第一档为月用电量200度（含）以内，第二档为月用电量200～320度（含），第三档为月用电量320度以上．这三个档次的电价分别为：第一档0.52元/度，第二档0.57元/度，第三档0.82元/度．若某户居民1月份用电250度，则应收电费：0.52×200+0.57×（250-200）=132.5元．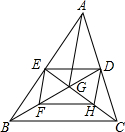
△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点，连接DE、EF、F、HD．