题目内容
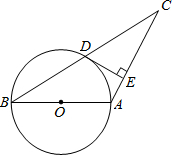 如图,AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E.
如图,AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E.(1)求证:DE是⊙O的切线;
(2)连结AD,若⊙O的半径为
| 5 |
| 2 |
考点:切线的判定
专题:计算题
分析:(1)连结OD、AD,如图,由圆周角定理得∠ADB=90°,则根据等腰三角形的性质得到BD=CD,所以可判断OD为△ABC的中位线,然后根据平行线的性质得到DE⊥OD,再根据切线的判定定理可得到结论;
(2)先利用勾股定理计算出BD=4,再证明Rt△ABD∽Rt△ADE,然后利用相似比可计算出DE的长.
(2)先利用勾股定理计算出BD=4,再证明Rt△ABD∽Rt△ADE,然后利用相似比可计算出DE的长.
解答:(1)证明:连结OD、AD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:在Rt△ABD中,∵AD=3,AB=5,
∴BD=
=4,
∵AD垂直平分BC,
∴AD平分∠BAC,
∴∠BAD=∠EAD,
∴Rt△ABD∽Rt△ADE,
∴
=
,即
=
,
∴DE=
.

∵AB为⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:在Rt△ABD中,∵AD=3,AB=5,
∴BD=
| AB2-AD2 |
∵AD垂直平分BC,
∴AD平分∠BAC,
∴∠BAD=∠EAD,
∴Rt△ABD∽Rt△ADE,
∴
| AB |
| AD |
| BD |
| DE |
| 5 |
| 3 |
| 4 |
| DE |
∴DE=
| 12 |
| 5 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理、等腰三角形的性质和相似三角形的判定与性质.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
下列调查中,宜采用全面调查的是( )
| A、对你所在的班级同学的身高的调查 |
| B、对长江流域的水污染情况的调查 |
| C、对某型号的节能灯的使用寿命的调查 |
| D、对我市合格食品的调查 |
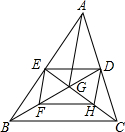 △ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,连接DE、EF、F、HD.
△ABC的两条中线BD与CE交于点G、F、H分别是BG、CG的中点,连接DE、EF、F、HD.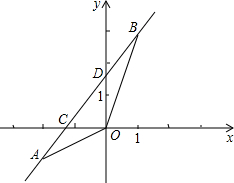 如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.