题目内容
8.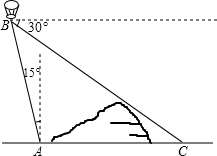 如图,在小山的西侧A处有一热气球,以25米/分钟的速度沿着与垂直方向所成夹角为15°的方向升空,40分钟后到达B处,这时热气球上的人发现,在A处的正东方向有一处着火点C,在B处测得着火点C的俯角为30°,求热气球升空点A与着火点C的距离.(结果保留根号)
如图,在小山的西侧A处有一热气球,以25米/分钟的速度沿着与垂直方向所成夹角为15°的方向升空,40分钟后到达B处,这时热气球上的人发现,在A处的正东方向有一处着火点C,在B处测得着火点C的俯角为30°,求热气球升空点A与着火点C的距离.(结果保留根号)
分析 在RT△ABD中求出AD,再在RT△ADC中求出AC即可解决问题.
解答 解:作AD⊥BC垂足为D,AB=40×25=1000,
∵BE∥AC,
∴∠C=∠EBC=30°,
∠ABD=90°-30°-15°=45°,
在Rt△ABD中,sin∠ABD=$\frac{AD}{AB}$,AD=ABsin∠ABD=1000×sin45°=1000×$\frac{\sqrt{2}}{2}$=500$\sqrt{2}$,
AC=2AD=1000$\sqrt{2}$,
答:热气球升空点A与着火点C的距离是1000$\sqrt{2}$米.
点评 本题考查解直角三角形的应用、俯角俯角、三角函数等知识,解题的关键是添加辅助线,构造直角三角形,记住三角函数的定义,以及特殊三角形的边角关系,属于中考常考题型.

练习册系列答案
相关题目
18.不等式组$\left\{\begin{array}{l}{5x-2<3(x+2)}\\{\frac{2x-1}{3}-\frac{5x+1}{2}≤1}\end{array}\right.$的最大整数解为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.窗花是我国传统民间艺术,下列窗花中,是轴对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
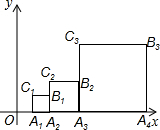 如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).
如图,正方形A1A2B1C1,A2A3B2C2,…Anan+1BnCn,如图位置依次摆放,已知点C1,C2,C3…,Cn在直线y=x上,点A1的坐标为(1,0).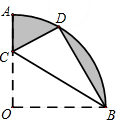 如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则有下列选项:
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,则有下列选项: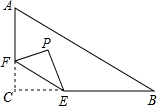 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是1.2.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是1.2.