题目内容
3.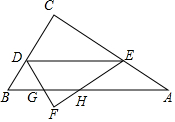 直角三角形ABC中,∠C=90度,CB=6,AC=8,D为CB边上一个动点,E为AC上一点,DE∥AB,将三角形CDE沿着DE翻折得到三角形DEF,设三角形DEF和三角形ABC重合的面积为y,DC=x,求y与x的函数关系式及定义域.
直角三角形ABC中,∠C=90度,CB=6,AC=8,D为CB边上一个动点,E为AC上一点,DE∥AB,将三角形CDE沿着DE翻折得到三角形DEF,设三角形DEF和三角形ABC重合的面积为y,DC=x,求y与x的函数关系式及定义域.
分析 分0≤x≤3和3<x≤6两种情况考虑,当0≤x≤3时,根据翻折变换结合三角形的面积即可得出y关于x的函数关系式;当3<x≤6时,利用分割图形求面积法结合三角形的面积即可得出y关于x的函数关系式.综上即可得出结论.
解答 解:当0≤x≤3时,点F在△ABC内(包括在边AB上),如图1所示,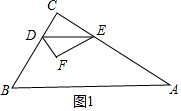
此时△DEF和△ABC重合部分是完整的△DEF.
由翻折的性质可知:△DEF≌△DEC.
∵DE∥AB,
∴$\frac{CD}{CB}=\frac{CE}{CA}$,
∴CE=$\frac{CD•CA}{CB}$=$\frac{4}{3}$CD=$\frac{4}{3}$x,
∴y=$\frac{1}{2}$CD•CE=$\frac{2}{3}$x2;
当3<x≤6时,点F在△ABC外,如图2所示.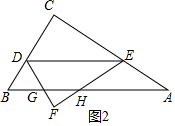
∵DE∥AB,
∴∠CDE=∠B,∠FGH=∠FDE.
由翻折的性质可知:∠CDE=∠FDE,
∴∠B=∠FGH=∠BGD,
∴BD=GD,
∴GF=2x-6,FH=$\frac{4}{3}$(2x-6),
∴y=S△CDE-S△FGH=$\frac{1}{2}$CD•CE-$\frac{1}{2}$GF•FH=-2x2+16x-24.
综上所述:y=$\left\{\begin{array}{l}{\frac{2}{3}{x}^{2}(0≤x≤3)}\\{-2{x}^{2}+16x-24(3<x≤6)}\end{array}\right.$.
点评 本题考查了根据实际问题列二次函数关系式、三角形的面积、平行线的性质以及翻折变换,分0≤x≤3和3<x≤6两种情况找出y关于x的函数关系式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.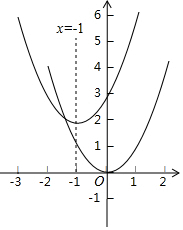 在学完《二次函数》后,老师给小明布置了家庭作业:完成下列表格,再用描点法在同一坐标系中画出y1与y2的函数图象.
在学完《二次函数》后,老师给小明布置了家庭作业:完成下列表格,再用描点法在同一坐标系中画出y1与y2的函数图象.
在同一坐标系内画出这两个函数的图象:小明已正确地完成作业(如图中抛物线y2的图象的对称轴为直线x=-1),由于不小心表格中的y2的解析式和部分数据被污渍覆盖了,请你根据作业单上的信息求出a,b,y2的解析式.
 在学完《二次函数》后,老师给小明布置了家庭作业:完成下列表格,再用描点法在同一坐标系中画出y1与y2的函数图象.
在学完《二次函数》后,老师给小明布置了家庭作业:完成下列表格,再用描点法在同一坐标系中画出y1与y2的函数图象.| x | … | 0 | 1 | 2 |
| y1=ax2 | … | 0 | 1 | 4 |
| y2=ax2+bx+c | … | 3 | 6 | 11 |
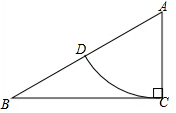 如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,以AC为半径画弧,交AB于D,则扇形CAD的周长是$\frac{π}{3}$+2(结果保留π)
如图,在△ABC中,∠ACB=90°,AC=1,AB=2,以A为圆心,以AC为半径画弧,交AB于D,则扇形CAD的周长是$\frac{π}{3}$+2(结果保留π)
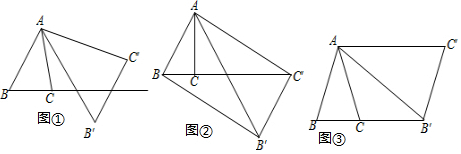
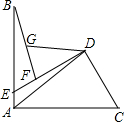 已知:AB=AC,DC=DF,∠BAC=∠CDF=90°,点G在BF上,
已知:AB=AC,DC=DF,∠BAC=∠CDF=90°,点G在BF上,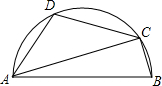 如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,$\widehat{AD}$=$\widehat{CD}$,求:∠BCD的度数.
如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=20°,$\widehat{AD}$=$\widehat{CD}$,求:∠BCD的度数.