题目内容
7.以方程组$\left\{\begin{array}{l}{y=2x+2}\\{y=-x+1}\end{array}\right.$的解为坐标的点(x,y)在第二象限.分析 先求出x、y的值,再根据各象限内点的坐标特点即可得出结论.
解答 解:$\left\{\begin{array}{l}y=2x+2①\\ y=-x+1②\end{array}\right.$,
∵①-②得,3x+1=0,解得x=-$\frac{1}{3}$,
把x的值代入②得,y=$\frac{1}{3}$+1=$\frac{4}{3}$,
∴点(x,y)的坐标为:(-$\frac{1}{3}$,$\frac{4}{3}$),
∴此点在第二象限.
故答案为:二.
点评 本题考查的是二元一次方程组的解,熟知各项限内点的坐标特点是解答此题的关键.

练习册系列答案
相关题目
15.若一个三角形的两边长分别为3和7,则第三边长可能是( )
| A. | 6 | B. | 3 | C. | 2 | D. | 11 |
16.计算(-x2y)2的结果是( )
| A. | x4y2 | B. | -x4y2 | C. | x2y2 | D. | -x2y2 |
 已知,如图,PA与⊙O相切于点A,过A作AB⊥OP,交⊙O于点B,垂足为H,连接OA,OB,PB.
已知,如图,PA与⊙O相切于点A,过A作AB⊥OP,交⊙O于点B,垂足为H,连接OA,OB,PB.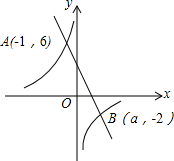 如图,一次函数y1=kx+b(k≠0)和反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于点A(-1,6),B(a,-2).
如图,一次函数y1=kx+b(k≠0)和反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于点A(-1,6),B(a,-2). 如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
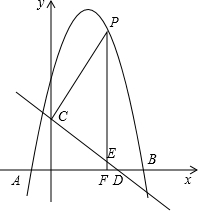 如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是第一象限内抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是第一象限内抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.