题目内容
8. 甲、乙两车分别从A、B两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到B地停止,乙车行驶到A地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为y(km),乙车行驶的时间为x(h),y与x之间的函数图象如图所示.
甲、乙两车分别从A、B两地沿同一路线同时出发,相向而行,以各自速度匀速行驶,甲车行驶到B地停止,乙车行驶到A地停止,甲车比乙车先到达目的地.设甲、乙两车之间的路程为y(km),乙车行驶的时间为x(h),y与x之间的函数图象如图所示.(1)求甲车行驶的速度.
(2)求甲车到达B地后y与x之间的函数关系式.
(3)当两车相遇后,两车之间的路程是160km时,求乙车行驶的时间.
分析 (1)甲车的速度是180÷1.8,即可解答;
(2)先求出乙车的速度是180-100=80km/h.a=180÷80=2.25,利用待定系数法即可求出函数解析式;
(3)当y=160时,求出x的值,即可解答.
解答 解:(1)甲车的速度是180÷1.8=100km/h.
(2)乙车的速度是180-100=80km/h.
a=180÷80=2.25.
设y与x之间的函数关系式为y=kx+b.
由题意,得$\left\{\begin{array}{l}{1.8k+b=144}\\{2.25k+b=180}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=80}\\{b=0}\end{array}\right.$,
则y=80x.
(3)当y=160时,80x=160,
解得:x=2.
答:乙车行驶的时间是2小时.
点评 本题考查了一次函数的应用,解决本题的关键是准确识图并获取信息.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.等腰△ABC的周长为10,则其腰长x的取值范围是( )
| A. | x>$\frac{5}{2}$ | B. | x<5 | C. | $\frac{5}{2}$<x<5 | D. | $\frac{5}{2}$≤x≤5 |
 如图所示,将矩形ABCD纸板剪出一个宽AE=5的矩形AEFD,再将它绕着中心O顺时针旋转,使其中两个顶点分别与点A和点F重合,得到矩形AMFN,再沿着直线AB向右平移使点M和点N分别落在边BC和边EF上,得到矩形GHIJ,当$\frac{AD}{AB}$=$\frac{5}{6}$时,矩形ABCD的长AB=15;宽AD=18.
如图所示,将矩形ABCD纸板剪出一个宽AE=5的矩形AEFD,再将它绕着中心O顺时针旋转,使其中两个顶点分别与点A和点F重合,得到矩形AMFN,再沿着直线AB向右平移使点M和点N分别落在边BC和边EF上,得到矩形GHIJ,当$\frac{AD}{AB}$=$\frac{5}{6}$时,矩形ABCD的长AB=15;宽AD=18. 如图,M为正方形ABCD边AB上一点,DN⊥DM交BC的延长线于点N.求证:AM=CN.
如图,M为正方形ABCD边AB上一点,DN⊥DM交BC的延长线于点N.求证:AM=CN.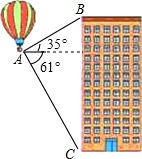 热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°,已知这栋楼BC的高度为300m,求热气球所在位置距地面的距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80)
热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°,已知这栋楼BC的高度为300m,求热气球所在位置距地面的距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80) 已知,如图,PA与⊙O相切于点A,过A作AB⊥OP,交⊙O于点B,垂足为H,连接OA,OB,PB.
已知,如图,PA与⊙O相切于点A,过A作AB⊥OP,交⊙O于点B,垂足为H,连接OA,OB,PB.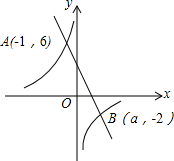 如图,一次函数y1=kx+b(k≠0)和反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于点A(-1,6),B(a,-2).
如图,一次函数y1=kx+b(k≠0)和反比例函数y2=$\frac{m}{x}$(m≠0)的图象交于点A(-1,6),B(a,-2).