题目内容
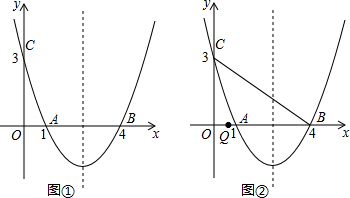
3.已知二次函数y=ax2+bx+c(a>0)经过点M(-1,8)和点A(1,0),交x轴另一点于B,交y轴于C.下列说法中:①b=-4;
②存在这样一个a,使得M、A、C三点在同一条直线上;
③抛物线的对称轴位于y轴的右侧;
④若a=1,则3OA•OB=OC2.
正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
分析 ①根据二次函数y=ax2+bx+c(a>0)经过点M(-1,8)和点A(1,0),因而将M、N两点坐标代入即可消去a、c解得b值;
②结合二次函数的图象即可判断M、A、C三点不在同一条直线上;
③求出二次函数图象对称轴方程x=-$\frac{b}{2a}$,结合a>0,b=-4即可作出判断;
④当y=0时利用根与系数的关系,可得到OA•OB的值,当x=0时,可得到OC的值.通过c建立等量关系求证.
解答 解:①∵二次函数y=ax2+bx+c(a>0)经过点M(-1,8)和点N(1,0),
∴$\left\{\begin{array}{l}{8=a-b+c}\\{0=a+b+c}\end{array}\right.$,
解得b=-4.
故该选项正确.
②根据抛物线图象的特点,M、A、C三点不可能在同一条直线上.
故该选项错误.
③由①可得b=-4,a>0,则对称轴x=-$\frac{b}{2a}$>0,
所以抛物线的对称轴位于y轴的右侧.
故该选项正确.
④当a=1时,c=3,∴该抛物线的解析式为y=x2-4x+3,
当y=0时,0=x2-4x+3,利用根与系数的关系可得x1•x2=3=c,
即OA•OB=3,
3OA•OB=OC2.
故该选项正确.
综上所述①③④正确.
故选C.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是要熟练掌握抛物线开口方向,对称轴以及根与系数关系等知识,此题难度不大.

练习册系列答案
相关题目
8.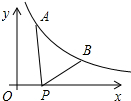 如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
 如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
如图所示,已知A(0.2,y1),B(2,y2)为反比例函数y=$\frac{1}{x}$ 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )| A. | (0.5,0) | B. | (1,0) | C. | (1.5,0) | D. | (2.5,0) |
16.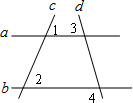 如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )
如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )
 如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )
如图,直线a、b与直线c、d相交,若∠1=∠2,∠3=70°,∠4的度数为( )| A. | 35° | B. | 70° | C. | 90° | D. | 110° |
 如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.
如图,已知等边△ABC,以AB为直径的圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.