题目内容
8．
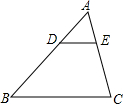如图，在△ABC中，DE∥BC，若AD=1，DB=2，则$\frac{DE}{BC}$的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
分析 由AD=1，DB=2，即可求得AB的长，又由DE∥BC，根据平行线分线段成比例定理，可得DE：BC=AD：AB，则可求得答案．
解答 解：∵AD=1，DB=2，
∴AB=AD+BD=1+2=3，
∵DE∥BC，
∴DE：BC=AD：AB=1：3=1：3．
故选C．
点评 此题考查了平行线分线段成比例定理．此题比较简单，注意掌握比例线段的对应关系是解此题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
3．下列计算正确的是（ ）
| A． | x4•x4=x16 | B． | （a3）2=a5 | C． | a+2a=3a | D． | （ab2）3=ab6 |
20．如果∠α=β，则∠α的补角比其余角大多少度？（ ）
| A． | 90° | B． | 60° | C． | 180° | D． | 45° |
17．
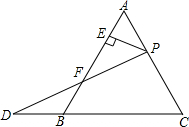已知等边三角形ABC的边长为12，点P为AC上一点，点D在CB的延长线上，且BD=AP，连接PD交AB于点E，PE⊥AB于点F，则线段EF的长为（ ）
已知等边三角形ABC的边长为12，点P为AC上一点，点D在CB的延长线上，且BD=AP，连接PD交AB于点E，PE⊥AB于点F，则线段EF的长为（ ）| A． | 6 | B． | 5 | C． | 4.5 | D． | 与AP的长度有关 |