题目内容
如果有理数满足|a-2|+(1-b)2=0,试求
+
+
+…+
的值.
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2003)(b+2003) |
考点:有理数的混合运算,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:根据|a-2|+(1-b)2=0,可求得a,b的值,再把
+
+
+…+
化简即可得出结论.
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2003)(b+2003) |
解答:解:∵|a-2|+(1-b)2=0,
∴a-2=0,且1-b=0,
解得a=2,b=1,
∴原式=
+
+
+…+
=1-
+
-
+
-
+••+
-
=1-
=
.
∴a-2=0,且1-b=0,
解得a=2,b=1,
∴原式=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2005×2004 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2004 |
| 1 |
| 2005 |
=1-
| 1 |
| 2005 |
=
| 2004 |
| 2005 |
点评:本题考查了有理数的混合运算以及非负数的性质,将原式拆成1-
+
-
+
-
+••+
-
是解题的关键.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2004 |
| 1 |
| 2005 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
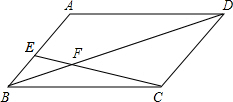 如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF的长为( )
如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,二次函数y=
如图,二次函数y=
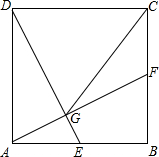 如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.
如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.
 如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第
如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第