题目内容
在一个不透明的口袋中有3个完全相同的小球,把它们分别标号为1,2,3,随机地取出一个小球然后放回,再随机地取出一个小球,则两次取出小球的标号的和是3的倍数的概率是 .
考点:列表法与树状图法
专题:常规题型
分析:列举出所有情况,看两次取出的小球的标号之和是3的倍数情况数占总情况数的多少即可.
解答:解:树状图如下:

共9种情况,两次取出的小球的标号之和是3的倍数的情况数有3种,
所以两次取出的小球的标号之和是3的倍数的概率为
=
.
故答案为:
.

共9种情况,两次取出的小球的标号之和是3的倍数的情况数有3种,
所以两次取出的小球的标号之和是3的倍数的概率为
| 3 |
| 9 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查概率的求法,用到的知识点为:概率=所求情况数与总情况数之比;得到两次取出的小球的标号之和是3的倍数的情况数是解决本题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
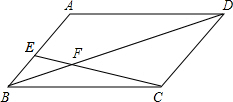 如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF的长为( )
如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
菱形ABCD的对角线AC=5,BD=10,则该菱形的面积为( )
| A、50 | ||||
| B、25 | ||||
C、
| ||||
| D、12.5 |

 如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第
如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图,当总用水量达到7000米3时,该经济作物种植时间是
某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图,当总用水量达到7000米3时,该经济作物种植时间是