题目内容
9.解方程:x2+3x-$\frac{20}{{x}^{2}+3x}$=8.分析 根据换元法:设u=$\frac{1}{{x}^{2}+3x}$,可得关于u的分式方程,根据解方程,可得答案.
解答 解:设u=$\frac{1}{{x}^{2}+3x}$,原方程等价于$\frac{1}{u}$-20u=8.
化简,得
20u2+8u-1=0.
解得u=$\frac{1}{10}$,u=-$\frac{1}{2}$.
当u=$\frac{1}{10}$时,x2+3x=10.解得x=-5,x=2,经检验x=-5,x=2是原分式方程的解;
当u=-$\frac{1}{2}$时,x2+3x+2=0.解得x=-1,x=-2,经检验:x=-1,x=-2是原分式方程的解;
综上所述:x=-5,x=2,x=-1,x=-2是原分式方程的解.
点评 本题考查了解分式方程,换元法是解题关键,要检验分式方程的解,以防产生增根,体现了化繁为简的化归转化思想.

练习册系列答案
相关题目
19.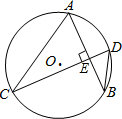 如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
 如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )
如图,AB、CD是⊙O弦,且AB⊥CD,若∠CDB=50°,则∠ACD的大小为( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
20.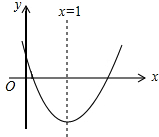 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )
 已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )
已知二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,下列结论中:①abc>0;②2a+b=0;③b2-4ac<0;④4a+2b+c>0;⑤3b<2c,其中正确的个数( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.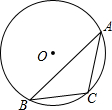 如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )
如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )
 如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )
如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
4.在下列说法中,错误的是( )
| A. | 无限小数都是无理数 | B. | 实数与数轴上的点一一对应 | ||
| C. | 无理数都是无限小数 | D. | 带有根号的数不都是无理数 |
 在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.
在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.