题目内容
15. 如图,直线y=-x+4与y=3x相交于点A,与x轴相交于点B,反比例函数$y=\frac{k}{x}$图象经过OA上一点P,PC⊥x轴,垂足为C,且S△AOB=2S△POC.
如图,直线y=-x+4与y=3x相交于点A,与x轴相交于点B,反比例函数$y=\frac{k}{x}$图象经过OA上一点P,PC⊥x轴,垂足为C,且S△AOB=2S△POC.(1)求A、B两点的坐标;
(2)求反比例函数的解析式.
分析 (1)将y=-x+4与y=3x联立组成方程组,求出方程组的解得到A点坐标;将y=0代入y=-x+4,求出x的值,进而得到B点坐标;
(2)先求出S△AOB=$\frac{1}{2}$×4×3=6,那么S△POC=3,再根据反比例函数比例系数k的几何意义求出|k|=2×3=6,结合图象确定k的值,即可得到反比例函数的解析式.
解答  解:(1)解方程组$\left\{\begin{array}{l}y=-x+4\\ y=3x\end{array}\right.$得,$\left\{\begin{array}{l}x=1\\ y=3\end{array}\right.$,
解:(1)解方程组$\left\{\begin{array}{l}y=-x+4\\ y=3x\end{array}\right.$得,$\left\{\begin{array}{l}x=1\\ y=3\end{array}\right.$,
所以A点坐标为(1,3).
解方程-x+4=0得,x=4,
所以B点坐标为(4,0);
(2)∵S△AOB=$\frac{1}{2}$×4×3=6,
∴S△POC=$\frac{1}{2}$S△AOB=$\frac{1}{2}$×6=3,
∴|k|=2×3=6.
由图象知k>0,即k=6,
所以反比例函数的解析式是y=$\frac{6}{x}$.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.同时考查了三角形的面积以及反比例函数比例系数k的几何意义.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
5. 如图,AB∥CD,E在AC的延长线上,若∠A=34°,∠DEC=90°,则∠D的度数为( )
如图,AB∥CD,E在AC的延长线上,若∠A=34°,∠DEC=90°,则∠D的度数为( )
 如图,AB∥CD,E在AC的延长线上,若∠A=34°,∠DEC=90°,则∠D的度数为( )
如图,AB∥CD,E在AC的延长线上,若∠A=34°,∠DEC=90°,则∠D的度数为( )| A. | 17° | B. | 34° | C. | 56° | D. | 124° |
3.下列计算正确的是( )
| A. | (a3)2=a5 | B. | $\sqrt{25}$=±5 | C. | $\root{3}{-8}$=-2 | D. | a6÷a2=a3 |
20.两个相似多边形的面积之比为1:9,则它们的周长之比为( )
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 2:3 |
7.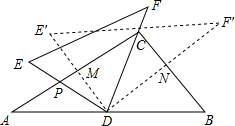 将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转α(0°<α<60°),DE′交AC于点M,DF′交BC于点N,则$\frac{PM}{CN}$的值为( )
将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转α(0°<α<60°),DE′交AC于点M,DF′交BC于点N,则$\frac{PM}{CN}$的值为( )
 将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转α(0°<α<60°),DE′交AC于点M,DF′交BC于点N,则$\frac{PM}{CN}$的值为( )
将一副三角尺(在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转α(0°<α<60°),DE′交AC于点M,DF′交BC于点N,则$\frac{PM}{CN}$的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{2}$ |
5. 如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
 如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )| A. | 50° | B. | 30° | C. | 20° | D. | 15° |
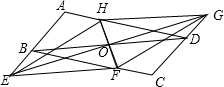 如图,过平行四边形ABCD的对角线BD的中点O作两条互相垂直的直线,且交AB、CD的延长线于点E,G,交BC,AD于点F,H,连接EF,FG,GH,EH.
如图,过平行四边形ABCD的对角线BD的中点O作两条互相垂直的直线,且交AB、CD的延长线于点E,G,交BC,AD于点F,H,连接EF,FG,GH,EH.
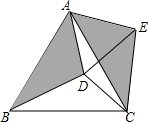 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.