题目内容
4.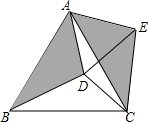 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.
分析 先根据等边三角形的性质得AB=AC,∠BAC=60°,再根据旋转的性质得AD=AE=5,∠DAE=∠BAC=60°,CE=BD=6,于是可判断△ADE为等边三角形,得到DE=AD=5;过E点作EH⊥CD于H,如图,设DH=x,则CH=4-x,利用勾股定理得到52-x2=62-(4-x)2,解得x=$\frac{5}{8}$,再计算出EH,然后根据正切的定义求解.
解答 解:∵△ABC为等边三角形,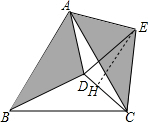
∴AB=AC,∠BAC=60°,
∵△ABD绕A点逆时针旋转得△ACE,
∴AD=AE=5,∠DAE=∠BAC=60°,CE=BD=6,
∴△ADE为等边三角形,
∴DE=AD=5,
过E点作EH⊥CD于H,如图,设DH=x,则CH=4-x,
在Rt△DHE中,EH2=52-x2,
在Rt△CHE中,EH2=62-(4-x)2,
∴52-x2=62-(4-x)2,解得x=$\frac{5}{8}$,
∴EH=$\sqrt{{5}^{2}-(\frac{5}{8})^{2}}$=$\frac{15\sqrt{7}}{8}$,
在Rt△EDH中,tan∠HDE=$\frac{EH}{DH}$=$\frac{\frac{15\sqrt{7}}{8}}{\frac{5}{8}}$=3$\sqrt{7}$,
即∠CDE的正切值为3$\sqrt{7}$.
故答案为:3$\sqrt{7}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质和解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.不等式2x<4的解集是( )
| A. | x<2 | B. | x<$\frac{1}{2}$ | C. | x>2 | D. | x>$\frac{1}{2}$ |
16.一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则一次性购买盒子所需要最少费用为29元.
| 型号 | A | B |
| 单个盒子容量(升) | 2 | 3 |
| 单价(元) | 5 | 6 |
13.荆州素有“鱼米之乡”的美称,某渔业公司组织20辆汽车装运鲢鱼、草鱼、青鱼共120吨去外地销售,按计划20辆汽车都要装运,每辆汽车只能装运同一种鱼,且必须装满,根据下表提供的信息,解答以下问题:
(1)设装运鲢鱼的车辆为x辆,装运草鱼的车辆为y辆,求y与x之间的函数关系式;
(2)如果装运每种鱼的车辆都不少于2辆,那么怎样安排车辆能使此次销售获利最大?并求出最大利润.
| 鲢鱼 | 草鱼 | 青鱼 | |
| 每辆汽车载鱼量(吨) | 8 | 6 | 5 |
| 每吨鱼获利(万元) | 0.25 | 0.3 | 0.2 |
(2)如果装运每种鱼的车辆都不少于2辆,那么怎样安排车辆能使此次销售获利最大?并求出最大利润.
 如图,直线y=-x+4与y=3x相交于点A,与x轴相交于点B,反比例函数$y=\frac{k}{x}$图象经过OA上一点P,PC⊥x轴,垂足为C,且S△AOB=2S△POC.
如图,直线y=-x+4与y=3x相交于点A,与x轴相交于点B,反比例函数$y=\frac{k}{x}$图象经过OA上一点P,PC⊥x轴,垂足为C,且S△AOB=2S△POC. 如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2$\sqrt{3}$为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A-B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2$\sqrt{3}$为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A-B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )



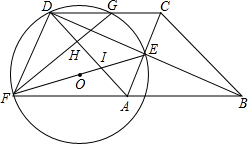 如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.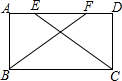 已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.
已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.