题目内容
6.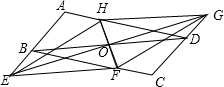 如图,过平行四边形ABCD的对角线BD的中点O作两条互相垂直的直线,且交AB、CD的延长线于点E,G,交BC,AD于点F,H,连接EF,FG,GH,EH.
如图,过平行四边形ABCD的对角线BD的中点O作两条互相垂直的直线,且交AB、CD的延长线于点E,G,交BC,AD于点F,H,连接EF,FG,GH,EH.(1)求证:△BEO≌△DGO;
(2)试判断四边形EFGH的形状,并说明理由.
分析 (1)由四边形ABCD是平行四边形,得到AB∥CD,由平行四边形的性质得到∠BEO=∠DGO,即可得到结论;
(2)由△BEO≌△DGO,得到OE=OG,由△BFO≌△DHO,得到OH=OF,于是得到四边形EFGH是平行四边形.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BEO=∠DGO,
在△BEO与△DGO中,
$\left\{\begin{array}{l}{∠BEO=∠DCO}\\{BO=DO}\\{∠BOE=∠DOG}\end{array}\right.$,
∴△BEO≌△DGO;
(2)由(1)证得△BEO≌△DGO,
∴OE=OG,
同理:△BFO≌△DHO,
∴OH=OF,
∴四边形EFGH是平行四边形.
点评 本题考查了全等三角形的判定和性质,平行四边形的判定和性质,掌握这些定理是解题的关键.

练习册系列答案
相关题目
17.某种细胞的直径是0.0005毫米,0.0005用科学记数法表示为( )
| A. | 5×104 | B. | 5×10-5 | C. | 5×10-3 | D. | 5×10-4 |
14.不等式2x<4的解集是( )
| A. | x<2 | B. | x<$\frac{1}{2}$ | C. | x>2 | D. | x>$\frac{1}{2}$ |
1. 如图所示的几何物体的左视图是( )
如图所示的几何物体的左视图是( )
 如图所示的几何物体的左视图是( )
如图所示的几何物体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
11. 如图,用19颗心组成的“大”字图案中不包含的变换是( )
如图,用19颗心组成的“大”字图案中不包含的变换是( )
 如图,用19颗心组成的“大”字图案中不包含的变换是( )
如图,用19颗心组成的“大”字图案中不包含的变换是( )| A. | 位似 | B. | 旋转 | C. | 平移 | D. | 轴对称 |
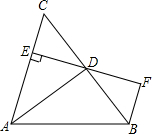 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( ) 如图,直线y=-x+4与y=3x相交于点A,与x轴相交于点B,反比例函数$y=\frac{k}{x}$图象经过OA上一点P,PC⊥x轴,垂足为C,且S△AOB=2S△POC.
如图,直线y=-x+4与y=3x相交于点A,与x轴相交于点B,反比例函数$y=\frac{k}{x}$图象经过OA上一点P,PC⊥x轴,垂足为C,且S△AOB=2S△POC.