题目内容
2.如图①,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,O是线段AB的中点,点D在线段AC上.(1)求证:△BCD≌△ACE;
(2)若M是线段BE的中点,N是线段AD的中点,求证:△MON是等腰直角三角形;
(3)将△DCE绕点C逆时针旋转α(0°<α<90°)后,记为△D1CE1(如图②),若M1 是线段BE1的中点,N1是线段AD1的中点,试猜测△M1ON1的形状.(要求直接写出结论,不要求证明)
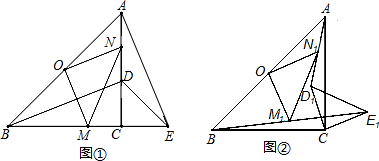
分析 (1)利用等腰直角三角形的性质得出CA=CB,CD=CE,再利用SAS证明三角形全等即可;
(2)延长BD交AE于H,BD与OM相交于G,再利用三角形中位线的定理OM=ON,进而证明等腰直角三角形即可;
(3)根据等腰直角三角形的判定得出△M1ON1是等腰直角三角形即可.
解答 解:(1)∵△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,
∴CA=CB,CD=CE,
在△BCD和△ACE中,
$\left\{\begin{array}{l}{CB=CA}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△ACE(SAS),
(2)延长BD交AE于H,设BD与OM相交于G,如图①,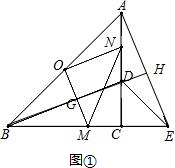
∵△BCD≌△ACE,
∴BD=AE,∠DBC=∠EAC,
又∵∠DBC+∠BDC=90°,∠BDC=∠ADH,
∴∠EAC+∠ADH=90°,
∴∠AHD=90°,
∵O是线段AB的中点,M是线段BE的中点,
∴OM∥AE且OM=$\frac{1}{2}$AE,
同理可证:ON∥BD,ON=$\frac{1}{2}$BD,
∴OM=ON,
∵OM∥AE,
∴∠BGO=∠AHD=90°,
∵ON∥BD,
∴∠MON=∠BGO=90°,
∴△MON是等腰直角三角形;
(3)延长BD1交AC于H,设BD1与OM1相交于G,如图②,
与(2)的证明相同得出△M1ON1是等腰直角三角形.
点评 此题考查几何变换问题,关键是根据等腰直角三角形的性质和判定进行分析,同时利用三角形的全等的判定解决问题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
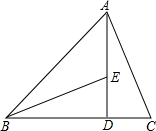 如图,在△ABC中,已知AD⊥BC于点D,点E在AD上,AD=BD,DE=CD,则BE和AC有何数量关系?试用学过的知识说明.
如图,在△ABC中,已知AD⊥BC于点D,点E在AD上,AD=BD,DE=CD,则BE和AC有何数量关系?试用学过的知识说明.