题目内容
如图，将抛物线y=| 1 |
| 3 |
| 1 |
| 3 |
考点：二次函数图象与几何变换
专题：
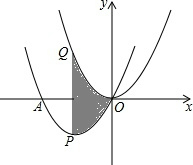
分析：连结OQ、OP，如图，先利用交点时写出平移后的抛物线m的解析式，再用配方得到顶点式y=（x+3）2-9，则P点坐标为（-3，-9），抛物线m的对称轴为直线x=-3，于是可计算出Q点的坐标为（-3，3），所以点Q与P点关于x轴对称，于是得到图中阴影部分的面积，然后根据三角形面积公式计算．
解答：
解：如图，连结OQ、OP，
平移后的抛物线解析式为y=（x+6）•x=x2+6x=（x+3）2-9，
所以P点坐标为（-3，-9），
抛物线m的对称轴为直线x=-3，
当x=-3时，y=
x2=3，则Q点的坐标为（-3，3），
由于抛物线y=
x2向左平移3个单位，再向下平移3个单位得到抛物线y=（x+3）2-9，
所以图中阴影部分的面积=S△OPQ=
×3×（3+3）=9．
故答案为9．
解：如图，连结OQ、OP，平移后的抛物线解析式为y=（x+6）•x=x2+6x=（x+3）2-9，
所以P点坐标为（-3，-9），
抛物线m的对称轴为直线x=-3，
当x=-3时，y=
| 1 |
| 3 |
由于抛物线y=
| 1 |
| 3 |
所以图中阴影部分的面积=S△OPQ=
| 1 |
| 2 |
故答案为9．
点评：本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
练习册系列答案
导学教程高中新课标系列答案
相关题目
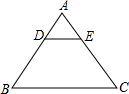如图，△ABC是等腰三角形，顶点为A、D、E分别在腰AB、AC上，连接DE，若△ADE是等腰三角形，且顶点为A，则下列结论中错误的是（ ）| A、AD=AE |
| B、BD=CE |
| C、DE∥BC |
| D、△ADE≌△ABC |
抛物线y=
（x-2）2+3的对称轴是直线（ ）
| 1 |
| 2 |
| A、x=-2 | B、x=2 |
| C、x=3 | D、x=-3 |
| 1 |
| 2 |
| 3 |
| 2015 |
| 5 |
| A、18个 | B、19个 |
| C、20个 | D、21个 |
如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=
九（1）班的同学来到“长征游乐园”举行发扬长征精神，重走长征路 系列的活动 过草地时，同学们遇到一片十几米宽的沼泽地，为了安全、迅速的通过这片沼泽地，他们沿着前进路线铺了若干块木板，构筑成一条临时通道，木板对地面的压强P（Pa）与木板的总面积S（m2）成反比例函数，其图象如图所示