题目内容
11.在△ABC中,∠C=90°,sinA=$\frac{3}{5}$,D是AB的中点,则tan∠BCD+tan∠ACD=( )| A. | $\frac{25}{12}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
分析 首先在△ABC中,由sinA=$\frac{BC}{AB}$=$\frac{3}{5}$,可设BC=3k,则AB=5k,利用勾股定理求出AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4k,那么tan∠B=$\frac{AC}{BC}$=$\frac{4k}{3k}$=$\frac{4}{3}$,tan∠A=$\frac{BC}{AC}$=$\frac{3k}{4k}$=$\frac{3}{4}$.再根据直角三角形斜边上的中线等于斜边的一半得出CD=BD=AD=$\frac{1}{2}$AB,由等边对等角得到∠BCD=∠B,∠ACD=∠A,所以tan∠BCD+tan∠ACD=tan∠B+tan∠A=$\frac{4}{3}$+$\frac{3}{4}$=$\frac{25}{12}$.
解答  解:∵在△ABC中,∠ACB=90°,
解:∵在△ABC中,∠ACB=90°,
∴sinA=$\frac{BC}{AB}$=$\frac{3}{5}$,
∴可设BC=3k,则AB=5k,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4k,
∴tan∠B=$\frac{AC}{BC}$=$\frac{4k}{3k}$=$\frac{4}{3}$,tan∠A=$\frac{BC}{AC}$=$\frac{3k}{4k}$=$\frac{3}{4}$.
∵在△ABC中,∠ACB=90°,D是AB的中点,
∴CD=BD=AD=$\frac{1}{2}$AB,
∴∠BCD=∠B,∠ACD=∠A,
∴tan∠BCD+tan∠ACD=tan∠B+tan∠A=$\frac{4}{3}$+$\frac{3}{4}$=$\frac{25}{12}$.
故选A.
点评 本题考查了解直角三角形,锐角三角函数定义,勾股定理,直角三角形斜边上的中线等于斜边的一半的性质,等边对等角的性质,根据条件得出∠BCD=∠B,∠ACD=∠A是解题的关键.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )
如图是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,使得两张图案构成的图形是中心对称图形.那么它至少旋转( )| A. | 30° | B. | 60° | C. | 120° | D. | 180° |
 如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )
如图,已知点A,B在半径为1的⊙O上,∠AOB=60°,延长OB至C,过点C作直线OA的垂线记为l,则下列说法正确的是( )| A. | 当BC等于0.5时,l与⊙O相离 | B. | 当BC等于2时,l与⊙O相切 | ||
| C. | 当BC等于1时,l与⊙O相交 | D. | 当BC不为1时,l与⊙O不相切 |
 如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )
如图,在△ABC中,DE∥BC,如果DE=2,BC=5,那么$\frac{AD}{DB}$的值是( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
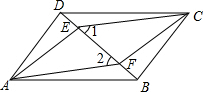 如图,四边形ABCD是平行四边形,E、F是对角线BD上的两点,∠1=∠2.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的两点,∠1=∠2.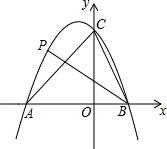 如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6).
如图,二次函数y=-x2-x+6的图象与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,点P是该图象上一点,且满足∠ABP=∠ACB,则点P的坐标是(-2,4)或(-4,-6).