题目内容
9. 某通讯公司推出甲、乙两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
某通讯公司推出甲、乙两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.(1)有月租费的收费方式是甲(填甲或乙),月租费是30元;
(2)求出甲、乙两种收费方式中y与自变量x之间的函数关系式.
分析 (1)由图象可知,甲图象中,当x=0时y=30,据此可得;
(2)结合图象,根据待定系数法可分别求得两函数解析式.
解答 解:(1)由图象可知,在甲图象中,当x=0时,y=30,
故有月租的收费方式是甲,月租费是30元;
(2)由图象可知,甲图象过(0,30),(300,60)两点,
设y甲=kx+b,
得:$\left\{\begin{array}{l}{b=30}\\{300k+b=60}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.1}\\{b=30}\end{array}\right.$,
故y甲=0.1x+30;
根据图象可知,乙图象经过原点(0,0),(300,60),
设y乙=mx,
将(300,60)代入求得:m=0.2,
故y乙=0.2x;
故答案为:(1)甲,30.
点评 本题考查了待定系数法求一次函数的解析式的运用,看懂函数图象是前提和基础,结合图象准确找到一次函数图象上的点是求解析式的根本.

练习册系列答案
相关题目
17.根据下面的表格,确定方程x2-8x+7.5=0的一个解的范围是( )
| x | 1.0 | 1.1 | 1.2 | 1.3 |
| x2-8x+7.5 | 0.5 | -0.09 | -0.66 | -1.21 |
| A. | 1.0<x<1.1 | B. | 1.1<x<1.2 | C. | 1.2<x<1.3 | D. | 1.0<x<1.3 |
4.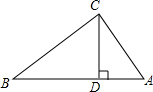 如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )
如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )
 如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )
如图,∠ACB=90°,CD是斜边上的高,AC=3,BC=4,则CD的长为( )| A. | 1.6 | B. | 2.4 | C. | 2 | D. | 2.1 |
14.若抛物线y=ax2经过A(1,-3),则下列各点中,在此抛物线上的是( )
| A. | (-3,1) | B. | (1,3) | C. | (-1,3) | D. | (-1,-3) |
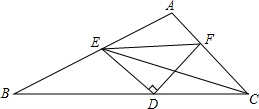 如图所示,在△ABC中,点E,F,D分别在线段AB,AC,BC上,并且满足∠DEF=∠DFE=∠BCA=45°,已知CF=6,CD=8,则线段EC的长为2$\sqrt{41}$.
如图所示,在△ABC中,点E,F,D分别在线段AB,AC,BC上,并且满足∠DEF=∠DFE=∠BCA=45°,已知CF=6,CD=8,则线段EC的长为2$\sqrt{41}$.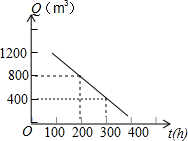 某水池贮满水后开始放水,t(h)后,水池中的水为Q(m3),Q与t的函数关系式如图所示.
某水池贮满水后开始放水,t(h)后,水池中的水为Q(m3),Q与t的函数关系式如图所示.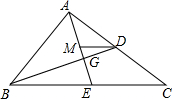 如图,△ABC的中线AE,BD交于点G,过点D作DM∥BC交AE于点M,则△AMD,△DMG和△BEG的面积之比为3:1:4.
如图,△ABC的中线AE,BD交于点G,过点D作DM∥BC交AE于点M,则△AMD,△DMG和△BEG的面积之比为3:1:4.