题目内容
14.若抛物线y=ax2经过A(1,-3),则下列各点中,在此抛物线上的是( )| A. | (-3,1) | B. | (1,3) | C. | (-1,3) | D. | (-1,-3) |
分析 先把点(1,-3)代入y=ax2得到a的值,确定抛物线解析式,然后分别计算自变量为-1,-3的函数值,再根据二次函数图象上点的坐标特征进行判断.
解答 解:把A(1,-3)代入y=ax2得a=-3,
所以抛物线解析式为y=-3x2,
当x=-1时,y=-3x2=-3;当x=-3时,y=-3x2=-27,
所以点(-1,-3)在抛物线上.
故选D.
点评 本题考查了待定系数法求二次函数的解析式以及二次函数图象上点的坐标特征,二次函数图象上点的坐标满足其解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列各组单项式中,是同类项的是( )
| A. | 5x2y与-3xy2 | B. | 8xy2与-2x2z | C. | 10abc与-8ab | D. | 5ab与-5ba |
2. 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )
 如图,数轴上点P表示的数可能是( )
如图,数轴上点P表示的数可能是( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
3.下列说法中正确的是( )
| A. | 0不是有理数 | B. | 有理数不是整数就是分数 | ||
| C. | 在有理数中有最小的数 | D. | a是有理数,则-a一定是负数 |
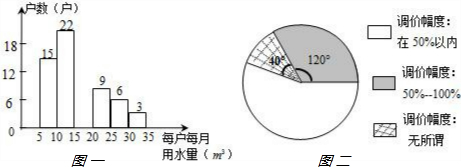
 某通讯公司推出甲、乙两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.
某通讯公司推出甲、乙两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.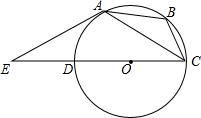 如图,⊙O是△ABC的外接圆,过点A作⊙O的切线与直径CD的延长线交于点E,已知AE=AC.
如图,⊙O是△ABC的外接圆,过点A作⊙O的切线与直径CD的延长线交于点E,已知AE=AC.