题目内容
11.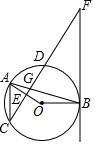 如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.(1)求证:FG=FB.
(2)若tan∠F=$\frac{3}{4}$,⊙O的半径为4,求CD的长.
分析 (1)根据等腰三角形的性质,可得∠OAB=∠OBA,根据切线的性质,可得∠FBG+OBA=90°,根据等式的性质,可得∠FGB=∠FBG,根据等腰三角形的判定,可得答案;
(2)根据平行线的性质,可得∠ACF=∠F,根据等角的正切值相等,可得AE,根据勾股定理,可得答案.
解答 (1)证明:∵OA=OB,
∴∠OAB=∠OBA,
∵OA⊥CD,
∴∠OAB+∠AGC=90°.
∵FB与⊙O相切,
∴∠FBO=90°,
∴∠FBG+OBA=90°,
∴AGC=∠FBG,
∵∠AGC=∠FGB,
∴∠FGB=∠FBG,
∴FG=FB;
(2)如图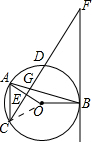 ,
,
设CD=a,
∵OA⊥CD,
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$a.
∵AC∥BF,
∴∠ACF=∠F,
∵tan∠F=$\frac{3}{4}$
tan∠ACF=$\frac{AE}{CE}$=$\frac{3}{4}$,即$\frac{AE}{\frac{1}{2}a}$=$\frac{3}{4}$,
解得AE=$\frac{3}{8}$a,
连接OC,OE=4-$\frac{3}{8}$a,
∵CE2+OE2=OC2,
∴($\frac{1}{2}$a)2+(4-$\frac{3}{8}$a)2=4,
解得a=$\frac{192}{25}$,
CD=$\frac{192}{25}$.
点评 本题考查了切线的性质,解(1)的关键是利用切线的性质得出∠FBG+OBA=90°,解(2)的关键是利用等角的正切值相等得出$\frac{AE}{\frac{1}{2}a}$=$\frac{3}{4}$,又利用了勾股定理.

练习册系列答案
相关题目
19.x7可以表示为( )
| A. | x3+x4 | B. | x3•x4 | C. | x14÷x2 | D. | (x3)4 |
20.下列交通标志中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.一次函数y=(2a-1)x+6的图象与坐标轴在第二象限围成的三角形的面积为6,则a的值为( )
| A. | a=2 | B. | a=-2 | C. | a=1 | D. | a=-1 |
 完成下列推理过程
完成下列推理过程
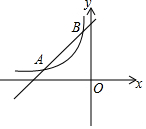 如图,直线y=kx+b与双曲线$y=\frac{m}{x}$(x<0)相交于A(-4,a)、B(-1,4)两点.
如图,直线y=kx+b与双曲线$y=\frac{m}{x}$(x<0)相交于A(-4,a)、B(-1,4)两点.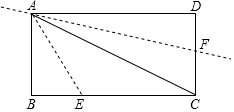 如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3$\sqrt{2}$,BC=3$\sqrt{6}$,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为2$\sqrt{3}$.
如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3$\sqrt{2}$,BC=3$\sqrt{6}$,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为2$\sqrt{3}$.