题目内容
1.一次函数y=(2a-1)x+6的图象与坐标轴在第二象限围成的三角形的面积为6,则a的值为( )| A. | a=2 | B. | a=-2 | C. | a=1 | D. | a=-1 |
分析 根据自变量与函数值的对应关系,可得三角形,根据三角形的面积,可得答案.
解答 解:当x=0时,y=6,
当y=0时,x=$\frac{6}{1-2a}$,
$\frac{1}{2}$×6(-$\frac{6}{1-2a}$)=6,
解得a=2,
故选:A.
点评 本题考查了一次函数图象上点的坐标特征,自变量与函数值的对应关系得出三角形是解题关键.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
12.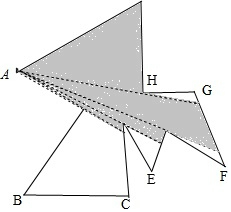 如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )
如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )
 如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )
如图,为了监控一不规则多边形艺术走廊内的活动情况,现已在A、B两处各安装了一个监控探头(走廊内所用探头的观测区域为圆心角最大可取到180°的扇形),图中的阴影部分是A处监控探头观测到的区域.要使整个艺术走廊都能被监控到,还需要安装一个监控探头,则安装的位置是( )| A. | E处 | B. | F处 | C. | G处 | D. | H处 |
9.据统计,2017年河南省的夏粮收购总产量为796.24亿斤,请用科学记数法表示这个数为( )
| A. | 7.9624×1010 | B. | 7.9624×109 | C. | 79.624×109 | D. | 0.79624×1011 |
16. 如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )
如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )
 如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )
如图,?ABCD中,AB=13,AD=10,将?ABCD沿AE翻折后,点B恰好与点C重合,则点C到AD的距离为( )| A. | 5 | B. | 12 | C. | 3 | D. | $\sqrt{69}$ |
6.已知三角形的三边长分别为a、b、c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式S=$\sqrt{p(p-a)(p-b)(p-c)}$,其中p=$\frac{a+b+c}{2}$;我国南宋时期数学家秦九韶(约1202-1261)曾提出利用三角形的三边求其面积的秦九韶公式S=$\frac{1}{2}$$\sqrt{{a}^{2}{b}^{2}-(\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2})^{2}}$,若一个三角形的三边长分别为2,3,4,则其面积是( )
| A. | $\frac{3\sqrt{15}}{8}$ | B. | $\frac{3\sqrt{15}}{4}$ | C. | $\frac{3\sqrt{15}}{2}$ | D. | $\frac{\sqrt{15}}{2}$ |
13.已知实数x、y满足(x-3)2+$\sqrt{y-7}$=0,则以x、y的值为两边长的等腰三角形的周长是( )
| A. | 13或17 | B. | 13 | C. | 17 | D. | 无法确定 |
10.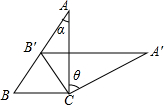 如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )
如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )
 如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )
如图,△ABC中,∠ACB=90°,∠A=α,以点C为中心将△ABC顺时针旋转θ角,得到△A′B′C′,且B′点恰好落在AB上,则旋转角θ的大小为( )| A. | α+10° | B. | α+20° | C. | α | D. | 2α |
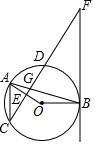 如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.
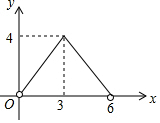
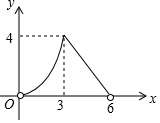
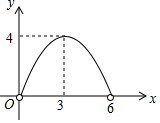
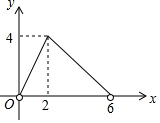
如图,点A、B、C、D均在⊙O上,FB与⊙O相切于点B,AB与CF交于点G,OA⊥CF于点E,AC∥BF.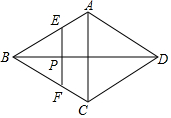 如图,在菱形ABCD中,AC=4,BD=6,P是BD上的任意一点,过点P作EF∥AC,与菱形的两条边分别交于点E、F.设BP=x,EF=y,则下列图象能大致反映y与x的函数关系的是( )
如图,在菱形ABCD中,AC=4,BD=6,P是BD上的任意一点,过点P作EF∥AC,与菱形的两条边分别交于点E、F.设BP=x,EF=y,则下列图象能大致反映y与x的函数关系的是( )