题目内容
如图,点A是半圆上一个三等分点,点B是 的中点,点P是直径MN上一动点,若⊙O的半径为1,则AP+BP的最小值是 .
的中点,点P是直径MN上一动点,若⊙O的半径为1,则AP+BP的最小值是 .

 .
.
【解析】作点A关于MN的对称点A′,连接A′B,交MN于点P,则PA+PB最小,
连接OA′,AA′.

∵点A与A′关于MN对称,点A是半圆上的一个三等分点,∴∠A′ON=∠AON=60°,PA=PA′,∵点B是弧AN^的中点,∴∠BON=30°,∴∠A′OB=∠A′ON+∠BON=90°,
又∵OA=OA′=1,∴A′B= .∴PA+PB=PA′+PB=A′B=
.∴PA+PB=PA′+PB=A′B= .
.

练习册系列答案
相关题目

 B.
B. C.
C. D.
D.


 ,
, ,
, ,…,根据你发现的规律计算:
,…,根据你发现的规律计算: =________(n为正整数).
=________(n为正整数). (1)此次抽样调查中,共调查了 名学生;
(1)此次抽样调查中,共调查了 名学生;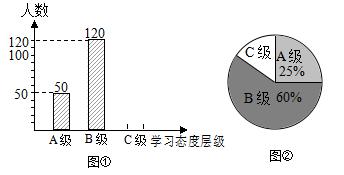

 的值.
的值. 与运行的水平距离x(m)满足关系式
与运行的水平距离x(m)满足关系式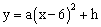 。已知球网与O点
。已知球网与O点 的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。 二次函数中二次项系数a的最大值。
二次函数中二次项系数a的最大值。