题目内容
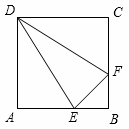
如图，在矩形ABCD中，AB=2，BC=4，⊙D的半径为1．现将一个直角三角板的直角顶点与矩形的对称中心O重合，绕着O点转动三角板，使它的一条直角边与⊙D切于点H，此时两直角边与AD交于E，F两点，则EH的值为 ．
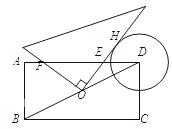
【解析】连接DH．
∵在矩形ABCD中，AB=2，BC=4，∴BD=
．∵O是对称中心，∴OD=
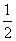BD=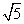
．
∵OH是⊙D的切线，∴DH⊥OH．∵DH=1，∴OH=2．∴tan∠ADB=tan∠HOD=．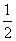
∵∠ADB=∠HOD，∴OE=ED．设EH为x，则ED=OE=OH-EH=2-x．∴12+x2=（2-x）2
解得=．即EH=
练习册系列答案
相关题目
=_______________．
个图形需 根火柴棒。
与一次函数
的图像相交于点A（-3,5），B（7，2），则能使
成立的x的取值范围是 
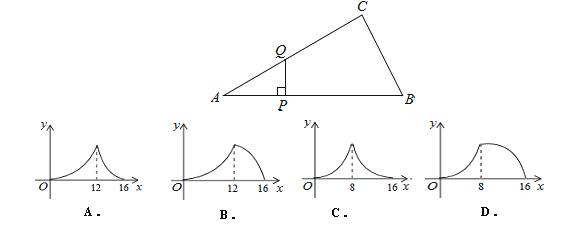
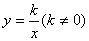的图象经过点（
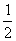，8），直线
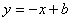经过该反比例函数图象上的点Q（4，
）．
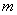轴、
轴分别相交于A 、B两点，与反比例函数图象的另一个交点为P，连结0P、OQ，求△OPQ的面积．
的中点，点P是直径MN上一动点，若⊙O的半径为1，则AP＋BP的最小值是 ．
