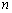题目内容
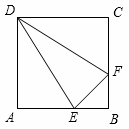
如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合.三角板的一边交CD于点F,另一边交CB的延长线于点G.

(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a,BC=b,请直接写出 的值.
的值.
( 1)证明见解析;(2)成立;证明见解析;(3)
1)证明见解析;(2)成立;证明见解析;(3)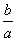 .
.
【解析】(1)∵∠GEB+∠BEF=90°,∠DEF+∠BEF=90°,∴∠DEF=∠GEB,
又∵ED=BE,∴Rt△FED≌Rt△GEB(ASA),∴EF=EG;
(2)成立,
如图,过点E分别作BC、CD的垂线,垂足分别为H、I,则EH=EI,∠HEI=90°,
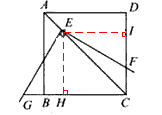
∵∠GEH+∠HEF=90°,∠IEF+∠HEF=90°,∴∠IEF=∠GEH,∴Rt△FEI≌Rt△GEH(ASA),
∴EF=EG;
(3)如图,过点E分别作BC、CD的垂线,垂足分别为M、N,则∠MEN=90°,
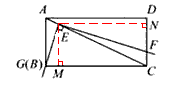
∴EM∥AB,EN∥AD,
∴△CEN∽△CAD,△CEM∽△CAB,
∴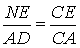 ,
,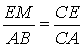 ,
,
∴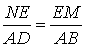 ,即
,即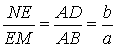 ,
,
∵∠NEF+∠FEM=∠GEM+∠FEM=90°,∴∠GEM=∠FEN,∵∠GME=∠FNE=90°,∴△GME∽△FNE,
∴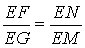 ,∴
,∴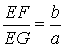 .
.

练习册系列答案
相关题目
 个图形需 根火柴棒。
个图形需 根火柴棒。
 的中点,点P是直径MN上一动点,若⊙O的半径为1,则AP+BP的最小值是 .
的中点,点P是直径MN上一动点,若⊙O的半径为1,则AP+BP的最小值是 .

 点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围. 表示大于
表示大于 x的
x的 最小整数,如
最小整数,如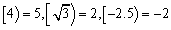 ,现对64进行如下操作:
,现对64进行如下操作: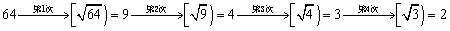 ,这样对64只需进行4次操作后变为2,类似地,
,这样对64只需进行4次操作后变为2,类似地, 最大的是 .
最大的是 . 0米的公路进行修建改造。根据需要,该工程在实际施工时增加了施工人员,每天修建的公路比原计划增加了50%,结果
0米的公路进行修建改造。根据需要,该工程在实际施工时增加了施工人员,每天修建的公路比原计划增加了50%,结果 提前4天完成任务。设现在每天修建x米,那么下面所列方程中正确的是【 】
提前4天完成任务。设现在每天修建x米,那么下面所列方程中正确的是【 】 。
。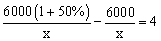 B.
B. 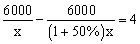
 D.
D. 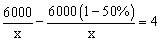





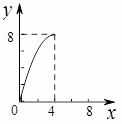

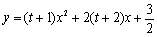
 , 在
, 在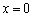
 和
和
 1)求二次函数的解析式;
1)求二次函数的解析式;
 的图象与二次函数的图象都经过点
的图象与二次函数的图象都经过点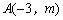
 ,求
,求
 和
和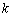
 的值;
的值; 设二次函数的图象与
设二次函数的图象与
 轴交于点
轴交于点
 (点
(点
 在点
在点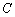
 的左侧),将二次函数的图象在点
的左侧),将二次函数的图象在点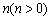
 个单位后得到的图象记为
个单位后得到的图象记为

 ,同时将(2)中得到的直线
,同时将(2)中得到的直线