题目内容
6.方程组$\left\{\begin{array}{l}{x-z=4}\\{z-2y=-1}\\{x+y-z=-1}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=-11}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-7}\\{y=5}\\{z=-11}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-7}\\{y=-5}\\{z=-11}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=7}\\{y=-5}\\{z=11}\end{array}\right.$ |
分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{x-z=4①}\\{z-2y=-1②}\\{x+y-z=-1③}\end{array}\right.$,
③-①得:y=-5,
把y=-5代入②得:z=-11,
把z=-11代入①得:x=-7,
则方程组的解为$\left\{\begin{array}{l}{x=-7}\\{y=-5}\\{z=-11}\end{array}\right.$,
故选C.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
17.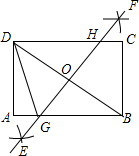 如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
 如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )| A. | $\frac{25}{8}$ | B. | $\frac{7}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{5}{8}$ |
14. 某班对四月联考数学试卷的10道选择题的答题情况进行统计,每道选择题的分值为3分,制成如图统计图.下列结论:①该班这10道选择题得分的众数为30分;②该班这10道选择题得分的中位数为30分;③该班这10道选择题得分的平均分为28.2分.其中正确结论的个数为( )
某班对四月联考数学试卷的10道选择题的答题情况进行统计,每道选择题的分值为3分,制成如图统计图.下列结论:①该班这10道选择题得分的众数为30分;②该班这10道选择题得分的中位数为30分;③该班这10道选择题得分的平均分为28.2分.其中正确结论的个数为( )
 某班对四月联考数学试卷的10道选择题的答题情况进行统计,每道选择题的分值为3分,制成如图统计图.下列结论:①该班这10道选择题得分的众数为30分;②该班这10道选择题得分的中位数为30分;③该班这10道选择题得分的平均分为28.2分.其中正确结论的个数为( )
某班对四月联考数学试卷的10道选择题的答题情况进行统计,每道选择题的分值为3分,制成如图统计图.下列结论:①该班这10道选择题得分的众数为30分;②该班这10道选择题得分的中位数为30分;③该班这10道选择题得分的平均分为28.2分.其中正确结论的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
11. 如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB=$\frac{3}{5}$,则AC的长为( )
如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB=$\frac{3}{5}$,则AC的长为( )
 如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB=$\frac{3}{5}$,则AC的长为( )
如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB=$\frac{3}{5}$,则AC的长为( )| A. | 3 | B. | 3.5 | C. | 4.8 | D. | 5 |
13.△ABC的三边满足|a+b-16|+$\sqrt{a-b-4}$+(c-8)2=0,则△ABC为( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
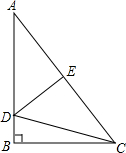 如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为$\frac{25}{8}$.
如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为$\frac{25}{8}$. 已知,如图,在△ABC中,AB=AC,以AC为直径作⊙O分别交AC,BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论:
已知,如图,在△ABC中,AB=AC,以AC为直径作⊙O分别交AC,BC于D、E两点,过B点的切线交OE的延长线于点F,连接FD,下列结论: