题目内容
11.已知|x-z+4|+|z-2y+1|+|x+y-z+1|=0,则x+y+z=9.分析 根据绝对值的非负性得出方程组,求出方程组的解,即可得出答案.
解答 解:∵|x-z+4|+|z-2y+1|+|x+y-z+1|=0,
∴$\left\{\begin{array}{l}{x-z+4=0①}\\{z-2y+1=0②}\\{x+y-z+1=0③}\end{array}\right.$
②+③×2得:2x-z=-3④,
由①④组成方程组$\left\{\begin{array}{l}{x-z+4=0}\\{2x-z=-3}\end{array}\right.$,
解得:x=1,z=5,
把z=5代入②得:y=3,
∴x+y+z=1+3+5=9.
故答案为:9.
点评 本题考查了绝对值的非负性,解三元一次方程组的应用,能得出三元一次方程组是解此题的关键.

练习册系列答案
相关题目
2.在整式5abc,-7x2+1,-$\frac{2x}{5}$,3.14,$\frac{4x-y}{2}$中,单项式共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.若-3xm-3ny8与28y5m+n的和仍是单项式,则有( )
| A. | $\left\{\begin{array}{l}{m=2}\\{n=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=-2}\\{n=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=1}\\{n=-\frac{7}{3}}\end{array}\right.$ |
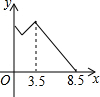
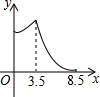
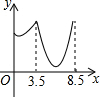
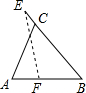 如图,在锐角△ABC中,BC=4,AB=3.5,E为BC延长线上一点,且BE=5,△ABC边上的动点F从点A出发,沿A→B→E的方向运动,到达点E时停止,设点F运动的路程为x,线段EF的长度的平方为y,则y关于x的函数的图象大致为( )
如图,在锐角△ABC中,BC=4,AB=3.5,E为BC延长线上一点,且BE=5,△ABC边上的动点F从点A出发,沿A→B→E的方向运动,到达点E时停止,设点F运动的路程为x,线段EF的长度的平方为y,则y关于x的函数的图象大致为( )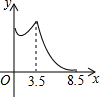

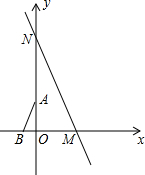 如图,在直角坐标系中,直线y=-$\sqrt{3}x+5\sqrt{3}$分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)或($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
如图,在直角坐标系中,直线y=-$\sqrt{3}x+5\sqrt{3}$分别与x轴、y轴交于点M、N,点A、B分别在y轴、x轴上,且∠B=60°,AB=2,将△ABO绕原点O顺时针转动一周,当AB与直线MN平行时点A的坐标为(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)或($\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).