题目内容
15.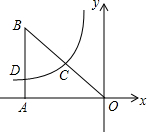 如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )
如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
分析 设B点坐标为(a,b),利用线段中点坐标公式得到C点坐标为($\frac{a}{2}$,$\frac{b}{2}$),再利用反比例函数图象上点的坐标特征得到k=$\frac{1}{4}$ab,得出反比例函数解析式为y=$\frac{ab}{4x}$,把D的横坐标代入求得纵坐标,即可求得$\frac{AD}{AB}$的值.
解答 解:设B点坐标为(a,b),
∵点C为斜边OB的中点,
∴C点坐标为($\frac{a}{2}$,$\frac{b}{2}$),
而点C在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴k=$\frac{1}{2}$a•$\frac{1}{2}$b=$\frac{1}{4}$ab,
∴反比例函数为y=$\frac{ab}{4x}$,
∵点D在反比例函数y=$\frac{k}{x}$(k≠0)上,D的横坐标为a,
∴D的纵坐标y=$\frac{ab}{4a}$=$\frac{b}{4}$,
∴D(a,$\frac{b}{4}$),
∴AD=$\frac{b}{4}$,
∴$\frac{AD}{AB}$=$\frac{1}{4}$.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征,待定系数法求解析式,求得C的坐标进而求得反比例函数的解析式是解题的关键.

练习册系列答案
相关题目
6.下列多项式中,不能在实数范围内因式分解的是( )
| A. | x2+$\sqrt{2}$x | B. | x2-$\sqrt{2}$x | C. | x2+$\sqrt{2}$ | D. | x2-$\sqrt{2}$ |
3.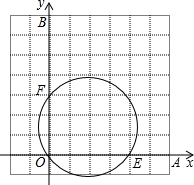 如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA,OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,0F=3个单位,则圆的直径为5个单位.
如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA,OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,0F=3个单位,则圆的直径为5个单位.
 如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA,OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,0F=3个单位,则圆的直径为5个单位.
如图,小华同学设计了一个圆直径的测量器,把标有刻度的尺子OA,OB在O点钉在一起,并使它们保持互相垂直.在测直径时,把O点靠在圆周上,读得刻度OE=4个单位,0F=3个单位,则圆的直径为5个单位.
7.据了解,单个禽流感H7N9病毒粒子的直径为0.0000001m,把10万个左右的病毒粒子排列起来才可能用肉眼勉强看得到.用科学记数法来表示该粒子的直径正确的是( )
| A. | 10-9m | B. | 10-8m | C. | 10-7m | D. | 10-6m |
4.下列命题中错误的是( )
| A. | 两组对边分别对应相等的四边形是平行四边形 | |
| B. | 两条对角线相等的平行四边形是矩形 | |
| C. | 两条对角线垂直的平行四边形是菱形 | |
| D. | 两条对角线垂直且相等的四边形是正方形 |
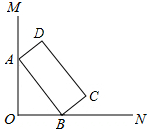 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,求运动过程中,点D到点O的最大距离.
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,求运动过程中,点D到点O的最大距离.