题目内容
5.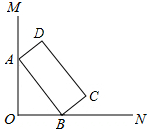 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,求运动过程中,点D到点O的最大距离.
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,求运动过程中,点D到点O的最大距离.
分析 取AB的中点E,连接OE、DE、OD,根据三角形的三边关系可知OD≤OE+DE,故当O、D、E三点共线时,点D到点O的距离最大,再根据勾股定理求出DE的长,由此可得出结论.
解答  解:如图,取AB的中点E,连接OE、DE、OD,
解:如图,取AB的中点E,连接OE、DE、OD,
∵OD≤OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵AB=2,BC=1,
∴OE=AE=$\frac{1}{2}$AB=1,
DE=$\sqrt{{AD}^{2}+{AE}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴OD的最大值为:$\sqrt{2}$+1.
点评 本题考查的是勾股定理,根据题意作出辅助线,构造出三角形,利用三角形的三边关系求解即可得出结论.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
15.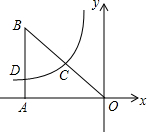 如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )
如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )
 如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )
如图,在平面直角坐标系xoy中,Rt△OAB的直角边在x轴的负半轴上,点C为斜边OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点C,且与边AB交于点D,则$\frac{AD}{AB}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{4}$ |
13.下列各数中,是无理数的是( )
| A. | -3.14 | B. | 0 | C. | $\frac{22}{7}$ | D. | $\sqrt{3}$ |
20.菱形的对角线长为8cm和6cm,则该菱形面积为( )
| A. | 48cm2 | B. | 24cm2 | C. | 25cm2 | D. | 14cm2 |




 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转15°.
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转15°. 某车间接到加工一批零件的任务,准备派甲、乙两名工人参与完成.乙比甲晚参加工作一段时间,工作期间甲工人因有事停工5天,若两人分得的工作量相等,各自的工作效率一定,他们各自的工作量y(个)随工作时间x(天)变化的图象如图所示,则有下列说法:
某车间接到加工一批零件的任务,准备派甲、乙两名工人参与完成.乙比甲晚参加工作一段时间,工作期间甲工人因有事停工5天,若两人分得的工作量相等,各自的工作效率一定,他们各自的工作量y(个)随工作时间x(天)变化的图象如图所示,则有下列说法: