题目内容
5.下列方程组中,是二元一次方程组的是( )| A. | $\left\{\begin{array}{l}{x+\frac{1}{3}=1}\\{y={x}^{2}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}3x-y=5\\ 2y-z=6\end{array}$ | C. | $\left\{\begin{array}{l}\frac{x}{5}+\frac{y}{2}=1\\ xy=1\end{array}$ | D. | $\left\{\begin{array}{l}\frac{x}{2}=3\\ y-2x=4\end{array}$ |
分析 根据二元一次方程组的定义进行判断即可.
解答 解:A、该方程组中未知数的最高次数是2,属于二元二次方程组,故本选项错误;
B、该方程组中含有3个未知数,属于三元一次方程组,故本选项错误;
C、该方程组中未知数的最高次数是2,属于二元二次方程组,故本选项错误;
D、该方程组符合二元一次方程组的定义,故本选项正确;
故选:D.
点评 本题考查了二元一次方程组的定义,把具有相同未知数的两个二元一次方程合在一起,就组成了一个二元一次方程组.

练习册系列答案
相关题目
15.下列长度的三条线段能组成三角形的是( )
| A. | 1 cm,2 cm,3.5 cm | B. | 4 cm,5 cm,9 cm | ||
| C. | 5 cm,8 cm,15 cm | D. | 6 cm,8 cm,9 cm |
16.下列命题中正确的个数是( )
| A. | 带根号的数是无理数 | B. | 无理数是开方开不尽的数 | ||
| C. | 无理数就是无限小数 | D. | 绝对值最小的数不存在 |
13.已知抛物线y=x2-x-2与x轴的一个交点为(m,0),则代数式m2-m+2014的值为( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
20.下列计算正确的是( )
| A. | $\sqrt{(-3)(-4)}$=$\sqrt{-3}$×$\sqrt{-4}$ | B. | $\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{{4}^{2}}$-$\sqrt{{3}^{2}}$ | C. | $\frac{\sqrt{6}}{2}$=$\sqrt{3}$ | D. | $\frac{\sqrt{6}}{\sqrt{2}}$=$\sqrt{3}$ |
10.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+1上的三点,则y1,y2,y3的大小关系为( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y3>y2>y1 | D. | y3>y1>y2 |
17.下列运算正确的是( )
| A. | 3x3-5x3=-2x | B. | 6x3-2x3=3x | C. | 3x(x-4)=3x2-12x | D. | -3(2x-4)=-6x-12 |
14.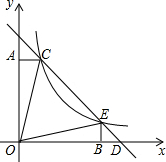 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:
①k的值为4;
②△BED是等腰直角三角形;
③S△ACO=S△BEO;
④S△CEO=15;
⑤点D的坐标为(5,0).其中正确的是( )
 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;
②△BED是等腰直角三角形;
③S△ACO=S△BEO;
④S△CEO=15;
⑤点D的坐标为(5,0).其中正确的是( )
| A. | ①②③ | B. | ①②③④ | C. | ②③④⑤ | D. | ①②③⑤ |
15.关于抛物线y=x2-2x+1,下列说法错误的是( )
| A. | 开口向上 | B. | 与x轴有一个交点 | ||
| C. | 对称轴是直线x=1 | D. | 当x>1时,y随x的增大而减小 |