题目内容
15.关于抛物线y=x2-2x+1,下列说法错误的是( )| A. | 开口向上 | B. | 与x轴有一个交点 | ||
| C. | 对称轴是直线x=1 | D. | 当x>1时,y随x的增大而减小 |
分析 把二次函数解析式化为顶点式,逐项判断即可得出答案.
解答 解:
∵y=x2-2x+1=(x-1)2,
∴抛物线开口向上,对称轴为x=1,当x>1时,y随x的增大而增大,
∴A、C正确,D不正确;
令y=0可得(x-1)2=0,该方程有两个相等的实数根,
∴抛物线与x轴有一个交点,
∴B正确;
故选D.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,其对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
5.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+\frac{1}{3}=1}\\{y={x}^{2}}\end{array}\right.$ | B. | $\left\{\begin{array}{l}3x-y=5\\ 2y-z=6\end{array}$ | C. | $\left\{\begin{array}{l}\frac{x}{5}+\frac{y}{2}=1\\ xy=1\end{array}$ | D. | $\left\{\begin{array}{l}\frac{x}{2}=3\\ y-2x=4\end{array}$ |
6.下列计算正确的是( )
| A. | $\sqrt{64}$的平方根为±8 | B. | $\sqrt{64}$的算术平方根为8 | ||
| C. | $\sqrt{64}$的立方根为2 | D. | $\sqrt{64}$的立方根为±2 |
20.如果a=-$\frac{1}{4}$,b=-2,c=-2$\frac{3}{\begin{array}{l}4\end{array}}$,那么|a|+|b|-|c|等于( )
| A. | -$\frac{1}{2}$ | B. | 1$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -1$\frac{1}{2}$ |
4.下列说法正确的是( )
| A. | 所有的有理数都能用数轴上的点表示 | |
| B. | 有理数分为正数及负数 | |
| C. | 0没有相反数 | |
| D. | 0的倒数仍为0 |
5.下列计算中,正确的是( )
| A. | ($\sqrt{3}$+$\sqrt{7}$)•$\sqrt{10}$=$\sqrt{10}$•$\sqrt{10}$=10 | B. | (6-2$\sqrt{3}$)(6+2$\sqrt{3}$)=36-6=30 | ||
| C. | (a$\sqrt{x}$+b$\sqrt{x}$)(a$\sqrt{x}$-b$\sqrt{x}$)=(a2-b2)x | D. | $\sqrt{6}$+$\sqrt{18}$=2$\sqrt{3}$+2$\sqrt{9}$=2($\sqrt{3}$+$\sqrt{9}$) |
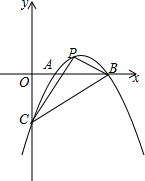 如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A、B,与y轴交于点C,点P为抛物线上一点,且∠PBO=∠CBO,求点P的坐标.
如图,抛物线y=-$\frac{2}{5}$x2+$\frac{12}{5}$x-2与x轴交于A、B,与y轴交于点C,点P为抛物线上一点,且∠PBO=∠CBO,求点P的坐标.