题目内容
 如图,⊙01和⊙O2外切,AB是外公切线,延长O1O2交AB的延长线于C点,若∠C=30°,AB=2,求两圆的半径.
如图,⊙01和⊙O2外切,AB是外公切线,延长O1O2交AB的延长线于C点,若∠C=30°,AB=2,求两圆的半径.考点:相切两圆的性质
专题:
分析:如图,作辅助线;证明四边形ABO2D为矩形,得到AD=O2B=μ,O1D=λ-μ;O2D∥AC,O2D=AB=2;列出关于λ、μ的方程组,求出λ、μ即可解决问题.
解答: 解:如图,连接O1A、O2B,过点O2作O2D⊥O1A;
解:如图,连接O1A、O2B,过点O2作O2D⊥O1A;
设⊙O1、⊙O2的半径分别为λ、μ;
∵AB是外公切线,
∴∠DAB=∠O2BA=90°,
∴四边形ABO2D为矩形,
∴AD=O2B=μ,O1D=λ-μ;O2D∥AC,O2D=AB=2;
∴∠DO2O1=∠C=30°;而⊙01和⊙O2外切,
∴O1O2=λ+μ;
由直角三角形的性质得:
,
解得:λ=
,μ=
,
即两圆的半径分别为
,
.
 解:如图,连接O1A、O2B,过点O2作O2D⊥O1A;
解:如图,连接O1A、O2B,过点O2作O2D⊥O1A;设⊙O1、⊙O2的半径分别为λ、μ;
∵AB是外公切线,
∴∠DAB=∠O2BA=90°,
∴四边形ABO2D为矩形,
∴AD=O2B=μ,O1D=λ-μ;O2D∥AC,O2D=AB=2;
∴∠DO2O1=∠C=30°;而⊙01和⊙O2外切,
∴O1O2=λ+μ;
由直角三角形的性质得:
|
解得:λ=
| 3 |
| ||
| 3 |
即两圆的半径分别为
| 3 |
| ||
| 3 |
点评:该题主要考查了相切两圆的性质及其应用问题;解题的关键是作辅助线,构造直角三角形,灵活运用勾股定理等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
在-3,
,π,0.35中,无理数是( )
| 1 |
| 2 |
| A、-3 | ||
B、
| ||
| C、π | ||
| D、0.35 |
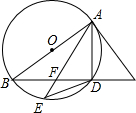 如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.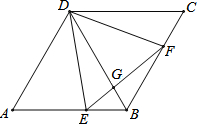 如图,在菱形ABCD中,∠A=60°,点E、F分别在边AB、BC上,EF与BD交于G,且∠DEF=60°.
如图,在菱形ABCD中,∠A=60°,点E、F分别在边AB、BC上,EF与BD交于G,且∠DEF=60°.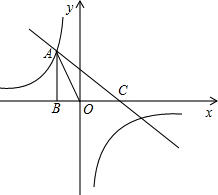 如图,已知反比例函数y1=
如图,已知反比例函数y1= 如图,∠CAB=90°,AD⊥BC,则∠CAD与∠B有何关系?并说明理由.
如图,∠CAB=90°,AD⊥BC,则∠CAD与∠B有何关系?并说明理由.